Mechanics and Relativity

Notes from Martin McCall's Lectures

Part I
Newton's Laws of Mechanic's

  1. A body remains at rest or moves with uniform velocity when no external force acts
    d
    dt
    		v=0 ÜÞ F=0
    'Law if Inertia' - Galileo: Constant velocity is the natrual state of motion
  2. The rate of change of momentum of a body is proportional to the force acting on the body
    F µ
    d
    dt
    		(mv)
    Most systems have constant mass (however rocket motion is one of many exceptions) in which case we can reduce this to:
    F µ m
    dv
    dt
    		µ ma
    Force unit is carefully chosen so that the constant of proportionality is 1. The Newton is the unit used for force where 1N causes an acceleration of 1ms-2 on a 1kg body First law is a special case of the second, since F=0, v=constant (ie first law)
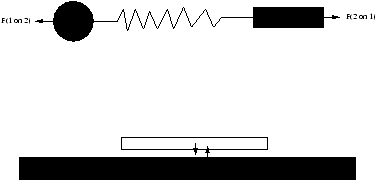
  3. When two bodies interact they exert on each other equal but opposite forces
    F1 on 2 = -F2 on 1
    From the third law
    d
    dt
    		(m1v1+m2v2)=0
    m1v1+m2v2=constant
    therefore conservation of momentum
Statement of Definition
define P=mv
Statement of Physics
momentum is conserved

Part II
One Dimensional Motion

Mathementical formulation of Newton II
F=ma
This is a vector equation however F is a vector sum of all the forces acting on a body.
Fx(x,y,z,x,y,z,t)=mx
Fy(x,y,z,x,y,z,t)=my
Fz(x,y,z,x,y,z,t)=mz
F may depend on: 7 variables have to be considered. Taking this into account the original equation is actually more complex.

Part III
Vibrational Motion

Part IV
Two Body Dynamics

Part V
Relativity

Part VI
Motion in 3-Dimensions

Part VII
Rigid Body Dynamics

Part VIII
Motion in Rotating Frames



This document was translated from LATEX by HEVEA and HACHA.