Previous Contents Next

Chapter 6   Basis

1-D: x, x=v, x=a, F
3-D: r,v=r, a=r, F

6.1   Work in 3-D

Recall 1-D: dW=Fdx , the work-energy theorem states that the work done by a force is equal to the changle in kinetic energy.

In 3-D its only the component of F along dl that contributes to the change in kinetic energy.
dW=F.dl=Fxdx+Fydy+Fzdz
So the total work in moving the particle from A to B along a particular path is
W= ó
õ
B


A
F.dl (along the path)
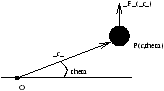
This is called a line integral, note this may be path dependent.

Consider a position dependent force ie the force vector F=F(r)¹ F(v)¹ F(t)
For F=F(r) consider components of F that are parallel and orthogonal to r . Tangential force (Fq.r=0) appears to turn the particle about O . What is the work done in rotating the particle from q to q+dq .

dW=Fxdx+Fydy=(turning effect)× dq ]
however |dl|=rdq
dx=-tdq × sin q =-ydq
dy=rdq × cos q =xdq
dW=-Fxydq +Fyxdq =[xFy-yFx]dq =(r× F)zdq

Define Torque as G=r× F but F=p so
G=r× p=r×
dr
dt
G=
d
dt
(r× p)¬¾
dr
dt
=0
G=
dr
dt
× p+r×
dp
dt
however dr/dt=v;  p=mv so dr/dt× p=0
G=
d
dt
(r× p)=L
where L=r× p is the Angular Momentum

Notes:
  1. G=d/dt(r× p)=L says that the torque equals the rate of change of momentum which is the angular analogue of Newton II
  2. although we have derived G and L using Fq a radial force component of Fr does not contribute as r× Fr=0

6.1.1   Radial Forces

Now F=f(r)r Examples of forces dependent on the magnitude of r : ie. forces at r originate from a source at the origin - Central Forces

Since the force is radial it has no turning effect about O (the source point)

ie. r× F=r× f(r)r=0 where F is purely radial so L=r× p=constant

For central forces the angular momentum is conserved [when we choose our origin to be the source point of the central forces]. For central forces the work done in moving from A to B is independent of the path taken
W= ó
õ
B


A
F× dl=-U(B)+U(A)
This is the definition of potential fir 3D forces (conservative ones)
ó
õ
B


A
F× dl = ó
õ
B


A
m
dv
dt
× dl = ó
õ
B


A
m
dl
dt
× dv = ó
õ
B


A
mvdv=
1
2
mvB2-
1
2
mvA2
ó
õ
B


A
F× dl=[ke @ B]-[ke @ A]
v2=v× v=vx2+vy2+vz2
2vdv=2v× dv=2vxdvx+2vydvy+2vzdvz

6.1.2   Work-Energy Theorem in 3D

W= ó
õ
B


A
F× dl=-U(B)+U(A)=[ke @ B]-[ke @ A]
E=(KE)A+U(A)=(KE)B+U(B)
conservation of mechanical energy in 3D

6.1.3   For Reference (see Prof. New's Maths Course)

F× dl=0 Û × F=0 [for central force]
= i
x
+j
y
+k
z

F =- U Û U=- ó
õ F× dl
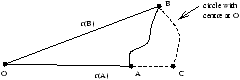
Calcuating òABF× dl
ó
õ
B


A
F× dl = ó
õ
C


A
F× dl + ó
õ
B


C
F× dl
1st term:
ó
õ
C


A
F.dl = ó
õ
rB


rA
F(r)dr
2nd term:
ó
õ
B


C
F.dl=0
since F is perpendicular to dl along the path C® B
W= ó
õ
B


A
F.dl = ó
õ
rB [=rC]


rA
F(r)dr

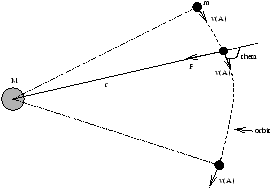
6.2   Orbits of Particles under Central Forces (eg gravity)

F=
-GmM
r2
r
Regard M» m
Work done by gravity in going from A to B
W= ó
õ
rB


rA
æ
ç
ç
è		 -
GmM
r2
ö
÷
÷
ø		 dr=
GmM
rB
-
GmM
rA
[=-U(B)+U(A)]
gravitational potential U(r)=-GmM/r so the work-energy theorem becomes
GmM
rB
-
GmM
rA
=
1
2
mvB2-
1
2
mvA2
conservation of energy
1
2
mvA2-
GmM
rA
=
1
2
mvB2-
GmM
rB
 [=E]
Angular Momentum
L=r× mv=constant for central forces
  1. since the direction of L is constant, motion is planar
  2. |L|=|r× mv|=mrvsin f
KE=
1
2
mv2=
1
2
m[v2cos2f +v2sin2 f]=
1
2
m[r2+
L2
m2r2
]
E=
1
2
mr2+
L2
2mr2
-
GmM
r
E=
1
2
mr2+U*(r)
ular momentum determines U*(r) . The total energy then determines the orbit where U*(r) is the pseudo potential that is seen by radial motion
U*(r)=
L2
2mr2
-
GmM
r
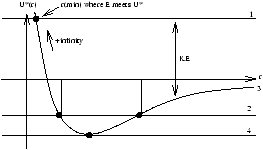
  1. there is a minimum value of r and the particle can escape to infinity
  2. particle confined between two points (ie bound)
  3. particle just escapes to ¥ (E=0)
  4. F=Umin* a circular orbit is only where this can occur
Once masses have been specified the angular momentum determines U*(r) . The total energy then determines the orbit
E=
1
2
mr2+
L2
2mr2
-
GmM
r
when E=U*(r) we have r=0

Case 1

E=
L2
2mrmin2
-
GmM
rmin
>0
with r=0
Ermin2+GmMrmin-
L2
2m
=0
rmin=
-GmM
2E
±
1
2E
. æ
ç
ç
è		 (GmM)2+
4EL2
2m
ö
÷
÷
ø
1
2



 
=
-GmM
2E
[1± æ
ç
ç
è		 (1+
2EL2
G2m3M2
ö
÷
÷
ø
1
2



 
]
since rmin>0 take the negative root
rmin=
GmM
2E
[(1+
2EL2
G2m3M2
)
1
2
 
-1]

Case 2

E=
L2
2mrmax/min2
-
GmM
rmax/min
<0
rmax/min=
-GmM
2E
[1± (1+
2EL2
G2m3M2
)
1
2
 
]
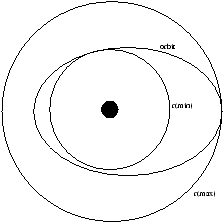
same equation as before, however as E is negative theco-efficient than becomes positive orbit is constrained between the limits rmin and rmin
Actual orbit turns out to be an ellipse, so we can work out the major axis (rmax+rmin)=GmM/E . In cartesian x2/a2+y2/a2(1-e2=1 .

If e (the eccentricity of the ellipse) is equal to zero then you get a circle, however if it is one then you get a line. The value of e lies between 0 and 1.
rmin/max=a(1 e)
compare to orbit formula
e= æ
ç
ç
è		 1+
2EL2
G2m3M2
ö
÷
÷
ø
1
2



 
where:
rmin
is the perihelim
rmax
is the aphelion

Case 3

L2
2mrmin2
-
GmM
rmin
=0 (E=0)
rmin=
L2
2Gm2M

Case 4

set U*/dr=0 -L2/mr3+GmM/r2=0
r0=
L2
Gm2M
 - circular orbit
v2
r0
=
GM
r02
; Emin=
-GmM
r0
orbital period is
T=
2p r0
v
=
2p r
3
2
 
0
GM

6.2.1   Notes

  1. closed orbit (elliptical) is a feature of 1/r potential. Other force laws also give bound orbits, but unclosed.
  2. deviations from ellipse mean
    1. take account of other bodies
    2. inverse square law is wrong! - but only very slightly wrong (due to relativistic effects)
  3. for E³ 0 trajectory is a parobala
so
e= æ
ç
ç
è		 1+
2EL2
G2m3M2
ö
÷
÷
ø
1
2



 
  1. E>0; e>1 hyperbola
  2. E<0; 0<e<1 ellipse
  3. E=0; e=1 parabola
  4. E=-G2m3M2/2L2; e=0 circle

6.3   Kepler's Laws (empirical)

  1. planets more in ellipses with the sun at a focas
  2. equal areas are swept out in equal times

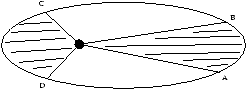
    the area swept out is the time from A to B is equal to the area swept out in the time from C to D

    t
     
    A® B
    		=t
     
    C® D
    A=
    1
    2
    		r2 q =
    1
    2
    		(r q )r
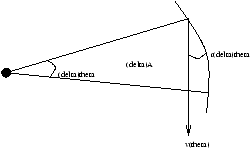
    so
    A
    t
    		=
    1
    2
    		r(r
    q
    t
    		)=
    1
    2
    		rv
     
    q
    L=mrv
     
    q
    ie dA/dt is a constant
  3. period and length for a closed loop orbit are related by
    T2µ L3
    where L is the radius of the cicular orbit or the semi-major axis (any scale distance)
Previous Contents Next