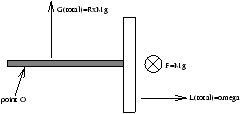Previous Contents Next

Chapter 7   Definition

Rigid means the different points of the body maintain their seperation

7.1   Torque and Angular Momentum for Systems of Particles

We had for a single particle
F=
dL
dt
where G=r× F (the torque) and L=r× p (the angular momentum).
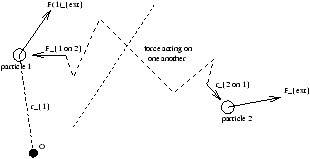
For particle 1: G1=r1× F1ext+r1× F12+r1× F13+...
For particle 2: G2=r2× F2ext+r2× F21+r2× F23+...
G (total torque)=G1+G2+...
Clearly this sum will involve terms like
r1× F12+r2× F21
but by Newton III F12=F21=f say that the contribution of such terms is
(r1-r2)× f
but (r1-r2) is parallel to f so
(r1-r2)× f=0
similar terms also vanish leaving
Gtotal=r1× F1ext+r2× F2ext+...
now we use Newton II F1ext=p1
Gtotal=r1× p1+r2× p2+... =
d
dt
[r1× p1+r2× p2+... ]=
d
dt
[L1+L2+... ]
Define Total Angular Momentum
Ltotal=L1+L2+...
Gtotal=
d
dt
Ltotal
note that for single particles Gtotal and Ltotal depend on the choice of origin

7.2   Calculation of Angular Mementum for a Rigid Body

Note for a single orbiting particle
G is not zero and L is not constant
Consider a rigid body rotating at a rate, w , about a fixed axis. Restrict to bodies that are uniform along the axis of arbitrary cross-section.

Rigid implies that all points rotate about the axis with equal angular speed dq/dt=w .

Choose the origin on the axis half way up the body. A typical volume element dV has mass r dV , where r is the mass density (which is uniform here). Therefore the contribution to angular momentum
dL=r× (dmv)=r r× rdV
L total= ó
õ (r× v)r dV

Integrated over the body, becuase of the choice of origin, the horizontal component of Ltotal vanishes. If x is radial distance fram axis then
|v|=v=w x
and
|r× r|=|r||v|sin q =w x2
so
L total= ó
õ (w x2)r dV=w I
where I=ò x2r dV and know as the moment of inertia so
Gtotal=
d
dt
Ltotal=I
dw
dt
=I
d2q
dt2
as vector equation Ltotal=Iw

7.3   Examples of Moments of Inertia

7.3.1   Rotating Rod

Uniform bar (rod) length D , sectional area A , rotating about its centre of mass
I= ó
õ
D
2


-
D
2
x2r Adx=r A
D3
12
where dV=Adx and dm=r (Adx)=r dV
But since rod is uniform
r =
M
AD
I=
MD2
12
eg. no external torque acting
Ltotal=Iw =constant
so a skater can increase w by changing D and hence I
1
12
MD12w1=
1
12
MD22w2

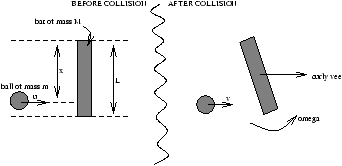
7.3.2   Ball Hitting Bat (exam April 1999)

from the last example
I(about centre of mass)=
1
12
ML2
Conservation of Linear Momentum
mu=mv+M
Conservation of angular momentum (the origin is at the centre of mass of the bat because the bat is uniform the centre of mass is at the centre of the bat)
mu(x-
L
2
)=mv(x-
L
2
)+Iw
NB the ball has angular momentum as it is offset from the centre of the bat
(mu-mv)(x-
L
2
)=
1
12
ML2w
where (mu-mv)=M . The velocity of the handle is equal to zero (when does this special case occur?)
-
w L
2
=0 =
w L
2
Mw L
2
(x-
L
2
)=
1
12
ML2w
x-
L
2
=
1
6
L Þ x=
L
2
+
L
6
=
2L
3
and this is the most comfortable position to hit the ball (know as the centre of percussion)

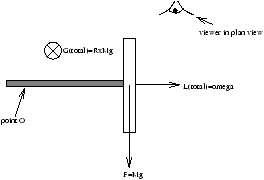
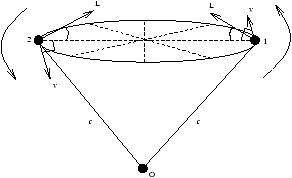
7.3.3   A Flywheel (or gyroscope)

view from above
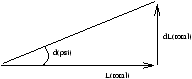
Now Gtotal=d/dtLtotal , in time dt
dLtotal=Gtotal× dt
dy ~
dL
Ltotal
dy =
MGR
Ltotal
dt=
MGRdt
Iw
W =
dy
dt
=
MGR
Iw
this is the rate the flywheel progresses when released with point O fixed, known as the processional angular frequency. Also the value of W can be obtained by:
dy =
dLtotal
Lw
=
Gtotal
Lw
dt=
RMg
Iw
dt
W =
dy
dt
=
RMg
Iw
Previous Contents Next