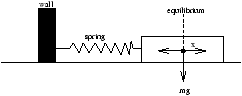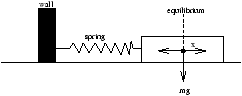Chapter 3 Vibrational Motion
-
vibrational systems are all around us. They are caused whenever an equilibrium system is disturbed
- waves represent oscillations in a continous medium (this is covered in Prof Dainty's Wave and Optics course)
3.1 Simple Harmonic Motion (SHM)
Prototype oscillator on a frictionless table and connected to a rigid wall
Force (Hooke's Law)=-kx; k=spring constant (units are kgs-2
By Newton II
mx+kx=0
let w 2=k/m
x+w 2x=0
A solution to this equation is Asin (w t) , however this is not a general solution.
Alternative (equilavent) form:
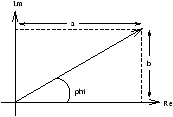
x=Asin (w t+f )
x=Acos p sin (w t) + A'sin f cos (w t)=Asin (w t)+Bcos (w t)
Motion is completely determined if we know two facts which allow us to calculate A' and f. eg we are told the initial conditions x and x at t=0.
Terminology:
-
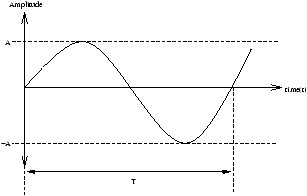
A
- amplitude
- w
- angular frequency
- T=2p/w
- period
- f=w/2p=1/T
- frequency
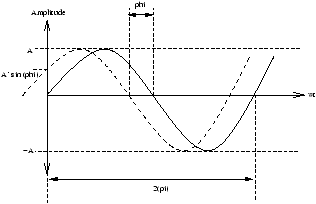
- (w t+f)
- phase (radius)
- f
- phase difference
3.1.1 Example
Mass 2kg (m) attached to a horizontal spring displaced by one millimetre (x0) from its equilibrium. Initially this displacement was caused by a force of 5N (F) and then released from rest. What is subsequent motion?
x=Asin (w t+f )
static extension: F=-kx0 used to calculate k
k=5× 103 Nm-1
Initial conditions: x=x0 at t=0
x0=Asin f
x=0 at t=0
x=w Acos f =0 at t=0
A=x0=10-3m
therefore the solution is x=10-3 sin (w t+p/2)=10-3cos (w t)
3.1.2 Energy of SHM Oscillations
x=Asin (w t+f )
Potential Energy U=-ò F dx=1/2mx2
Kinetic Energy K=1/2mv2=1/2mx2
Total Energy E=U+K
| E= |
|
m[w Acos (w t+f)]2+ |
|
k[Asin (w t+f )]2 |
| E= |
|
mw 2A2cos 2(w t+f)+ |
|
mw 2A2sin 2(w t+f )= |
|
kA2= |
|
mw 2A2=constant |
3.2 Damped Oscillations
This type of oscillation is a none conservative force (eg friction) due to energy being lost to the particles surroundings, therefore the amplitude of the oscillation will decrease with time.
Viscous force such that Fresistive=-bv-b(-x)=bx-bv
by Newton II: mx=-kx-bx
x+g x+w 02x=0
where w 2 =k/m and g =b/m
-
experience shows us that with (light) damping the mass oscillates
- also, the amplitude decays with time
Try a solution that includes both these features
x=Ae-qtcos (w t+f )
substitute this into x+g x+w 02x=0
x=-w Ae-qtsin (w t+f )-qAe-qtcos (w t+f )
|
x |
= |
-w 2Ae-qtcos (w t+f )+qw Ae-qt sin (w t+f )+ |
|
|
|
|
+qw Ae-qtsin (w t+f )+q2Ae-qtcos (w t+f) |
|
[-w 2+q2-g q+w 02]Ae-qtcos (w t+f )+[2qw -g w )Ae-qtsin (w t+f )º 0
if sin (w t+f )=0 or 1
if cos (w t+f )=1 or 0
-w 2+q2-g q+w 02=0
w < w 0 (or T > T0 damping increaseing period
There are two time constants associated with damped SHM.
-
The Natural Period: T0=2p/w 0
- The Decay Time Constant: T0=1/g
We will find that many of the features of damped SHM depend on the ration of T0 and TD
High QÞ TD» T0 so the system goes through many cycles before decaying.
Some examples are listed in the table.
| |
Q |
w 2 |
g |
| pendulum |
102 |
1 |
10-2 |
| tuning fork |
104 |
103 |
10-1 |
| FM tuning circuit |
104 |
108 |
104 |
| excited atom |
107 |
1015 |
108 |
| |
3.2.1 What about Energy
We know that the energy is proportional to the (amplitude)2
Now x=Ae-g t/2cos (w t+f ) Eµ A2e-g t
But the initial energy E at t=0
Energy decays with time constant T0
3.2.2 Energy Loss per Cycle
| E(t+T)=E(0)e |
|
=E(0)e |
|
e |
|
=e(t)e |
|
For light damping g T« 1 however T~ T0
D E=E(t)[1-(1-g T0)]=E(t)g T0
ie the fraction of energy loss per cycle
the energy loss per radian is 1/Q
the alternative definition of Q factor is:
| Q= |
| Energy Stored in Oscillator |
|
| Energy Loss Per Radian |
|
3.2.3 Possible Damping Scenerio's
-
light damping
- so far assume w 02>g/2 and so the system oscillates but the amplitude decays with time
- heavy damping (overdamping)
- w 0<g/2 where w is imaginary.
set f =0 (for example)
| Þ x=Ae |
|
[ |
|
(e |
|
+e |
|
)]= |
|
(e |
|
+e |
|
) |
-
a1
- = g/2+a =g/2+( g/2 ) 2-w 02
- a2
- = g/2-a =g/2-( g/2 ) 2-w 02
system moves back to equilibrium without oscillating. The time constants are given by (a1-1,a2-1)
- critical damping
- w 02=g/2 Þ w =0
this represents the fastest return to equilibrium, often used in mechanical suspension systems in cars.
3.3 Forced Oscillations
Sometimes you want to sustain oscillation in presence of damping
Equation of Motion
where:
-
g
- =b/m
- w
- =k/m
ie Inhomogenous
There are two methods for finding the particular solution to a forced harmonic oscillators
-
rotating line method
- complex number method
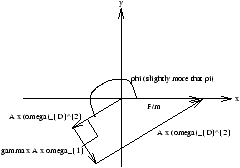
3.3.1 Rotating Line Method
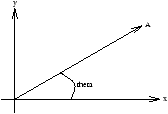
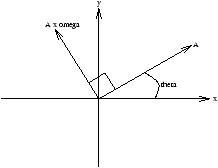
x=Asin q where q =w t+f
| x=-w 0Asin (w Dt+f )=+w DAcos (w Dt+f+ |
|
) |
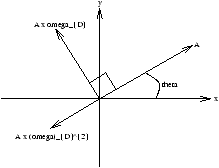
x=wD2Acos (w Dt+f )=w D2Acos (w t+f +p )
The rotating lines representing x, x, x, F must add (as vectors) together for a closed quadrataleral
Equate horizontal and vertical components
| « : |
|
=w D2Acos f -g w DAsin f -w F2Acos f |
: 0=w 22Asin f +g w 2Acos f -w 22Asin f
3.3.2 Complex Number Method
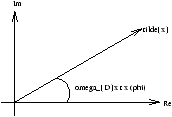
Define x such that x=Â [x] , now set x=Ae (wDt+f )=Ae wDt
where: A =Ae f the complex amplitude
where: F=Fe w D t
Original real oscillator equation is recovered by taking the real part.
Substitute these back into the original real oscillator equation:
| |
| F/m |
|
| [(w 02-w D2)2+g 2 w D2] |
|
× |
| [(w 02-w D2)2+g 2 w D2] |
|
| [(w 02-w D2)2+g 2 w D2] |
|
| x=Â [x]=Â [A |
e |
|
]=Â [Ae |
|
]=Acos (w Dt+f ) |
3.3.3 The General Solution
is the sum of
A0cos (w Dt+f )
where w = [w 02-(g/2)2]1/2
for example
| x=A0e |
|
cos (w t+f 0)+Acos (w Dt+f )=(transient) + (steady state) |
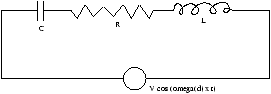
3.3.4 Electrical Analogue
mx+bx+kx=Fcos (w Dt )
where:
-
m
- ® L (inductance)
- b
- ® R (resistance)
- k
- ® 1/C ([Capacitance]-1)
- F
- ® V (voltage)
steady state solution
q=q0cos (w Dt+f )
where:
3.3.5 Power Developed in Forced SHM
Power transfered to mass/charge by driving force
power (P) = Force (F) x Velocity (V)
Driving Force = Fcos (w Dt)
Velocity of Mass (x)=-w DAsin (w Dt+f
| P(t)=-wDAFsin (w Dt+f )cos (w Dt)= |
|
[sin (2w Dt+f )+sin f ] |
| 1st Term ~ |
|
ó
õ |
|
sin (2w Dt+f ) dt=0 |
Power transferred to oscillating system is a maximum when f = p/2 at which point w D=w0
This occurs when force is in quadrature with the displacement.
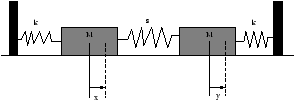
3.4 Coupled Oscillations
Both masses are displaced from equilibrium, their equations of motion are:
mx=-kx+s(y-x)
my=-s(y-x)-ky
or:
where: w 02º k/m
We know that x=Acos (w t+f ) and x=-w 2Acos (w t+f )
x=-w 2x
seek the solutions where both masses oscillate at the same frequency, this is know as the Normal Mode.
x=-w 2x
y=-w 2y
substitute this into equations of motion:
now we have two linear simutaneous equations with two unknowns.
This is analougous to a graph style solution the equations ax+by=0 and cx+dy=0 where x=y=0 which gives us the Trivial Solution (unuseful). However if this means instead that the two lines coincide (i.e. line 2 is proportional to line 1) a more useful answer can be obtained from the Trivial Solution.
In our case
If ad-bc=0 :
| (w 2)2-2(w 02+ |
|
)w 2+(w 02+ |
|
)2-( |
|
)2=0 |
second solution : w 22=w 02+2s/m
-
Mode 1: w 1=w 0
-
substitute back into the linear equation for x and y .
| (-w 02+w 02)x- |
|
(y-x)=0 Þ x=y |
- Mode 2: w 2=(w 02+2s/m)1/2
-
| -(w 02+ |
|
)x+w 02x- |
|
(y-x)=0 |
-
for mode 1:
-
x=Acos (w 1t+f 1) [=y]
y=Acos (w 1t+f 1) [=x]
- for mode 2:
-
x=Bcos (w 2t+f 2) [=-y]
y=-Bcos (w 2t+f 2) [=-x]
so as a general solution:
x=Acos (w 1t+f 1)+Bcos (w 2t+f 2)
y=Acos (w 1t+f 1)-Bcos (w 2t+f 2)
where A,B, f 1, f 2 are four arbitrary constants that are required for the general solution.
3.4.1 Example
x=a, y=0, x=y=0 at t=0 show that f 1=f 2=0 and A=B=-a/2
x=acos wtcos (¶ w t)
y=asin wtsin (¶ w t)
where:
-
w
- =w 1+w 2/2
- ¶ w
- =w 2-w 1/2
3.4.2 Beats
-
both masses oscillate at w . The amplitude grows to a maximum and then falls to a minimum
- enery is transfered from mass 1 to mass 2 (and back again, and again, and again ...) at the beat frequency ¶ w
Total Energy (E) = (Energy in Mode 1) + (Energy in Mode 2)
energy for one SHM mass = 1/2mw 2A2
if no mode 2 E=2× 1/2mw 12A2
if no mode 1 E=2× 1/2mw 22B2
| E1+2=2× |
|
mw 12A2+2× |
|
mw 22B2 |
| E= |
|
m(w 12+w 22)a2= |
|
(k+s)a2 |
| [ k+s=w 12+w 22=w 02+w 02+ |
|
=2(w 02+ |
|
) ] |