


| F=m |
|
|
=x=constant=a |
|
æ è |
ó õ a dt = |
ö ø |
|
=v=x=v0+at |
|
æ è |
ó õ v dt = |
ö ø |
x=x0+v0t+ |
|
at2 |
| F=m |
|
| ó õ |
|
F dx=m | ó õ |
|
|
dx |
| ó õ |
|
F dx=m | ó õ |
|
v dv |
| F | ó õ |
|
dx=m | ó õ |
|
v dv |
| F(x-x0)= |
|
mv2- |
|
mv02 |
| K= |
|
mv2 |
| p=mv K= |
|
| ó õ |
F dt= | ó õ m |
|
dt |
| F | ó õ |
|
dt=m | ó õ |
|
dv |
| P= |
|
=F |
|
| W= | ó õ |
|
Fz dz= | ó õ |
|
-mg dz=-mg(z-z0)=-mgh |
| ó õ |
|
m |
|
dx= | ó õ |
|
F(x) dx |
|
mv2- |
|
mv02= | ó õ |
|
F(x) dx=D K (work done by F) |
| F(x) º |
|
|
mv2- |
|
mv02=-U(x)+U(x0) |
|
mv2+U(x)= |
|
mv02+U(x0)=E |
|
= |
|
( |
|
mv2)+ |
|
U(x)=mv |
|
+ |
|
|
=Fv+(-F)v=0 |

|
mv2- |
|
mv02= | ó õ |
|
F(z) dz |
| F(z)= |
|
|
mv2= | ó õ |
|
|
dz= |
|
|
mv2= |
|
| v= |
|
| Force= |
|
=-( |
|
= |
|
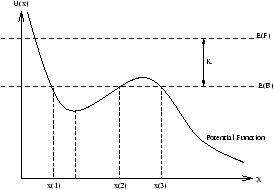
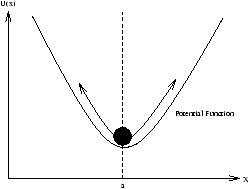
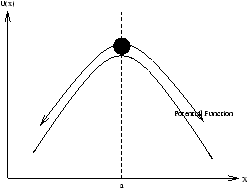
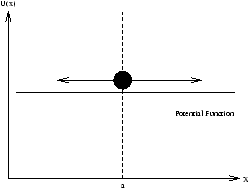
| U(x)=U(a)+U'(a)(x-a)+ |
|
U''(a)(x-a)2+... |
| U(x)~ U(a)+ |
|
U''(a)(x-a)2 |
| U(X)=U(0)+ |
|
U''(0)X2 |
| F= |
|
=-U''(0)X=-kX |
| U(x)=U(a)+U'(a)(x-a)+ |
|
U''(a)(x-a)2+... |
| U(X)=U(0)+ |
|
U''(0)X2 |
| F= |
|
=-U''(0)X |
| w= |
|
= |
|
| T= |
|
=2p |
|
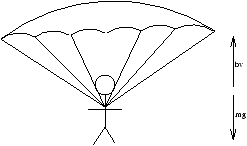
| mg-bv=m |
|
| ó õ |
|
|
= | ó õ |
|
dt |
| - |
|
ln [mg-bv]0v=t |
| v= |
|
[1-e |
|
] |
| v |
|
=v |
|
=terminal velocity |
| v=v |
|
[1-e |
|
] |
|
æ è |
ó õ v dt=x(t) |
ö ø |


