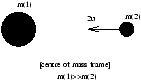Chapter 4 Motion

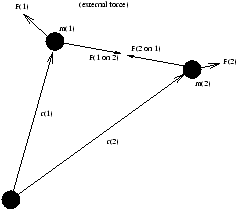
m₁r₁=F_1 on 2+F₁^external

m₂r₂=F_2 on 1+F₂^external

But F_1 on 2=-F_2 on 1 by Newton III

m₁r₁+m₂r₂=F₁^external+F₂^external=F^external

Define

Rº

m₁r₁+m₂r₂

where M=m₁+m₂

MR=m₁r₁+m₂r₂=F^external

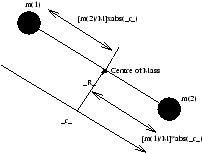
R defines the centre of mass of m₁ and m₂ and the centre of mass follows Newtons II law with respect to the external force; blind to the internal force. eg External Force = Uniform Gravity

MZ=m₁g+m₂g=Mg

Z=g

Internal Motion
Set F^external=0 so it is an isolated system

Þ MR=0 Þ MR=k

therefore this is true and momentum is conserved in an isolated system. Now

m₁r₁=F_1 on 2º F^internal

m₂r₂=F_2 on 1=-F_1 on 2

Þ r₂-r₁=

F_2 on 1

m₂

F_1 on 2

m₁

æ
ç
ç
è

m₁

m₂

ö
÷
÷
ø

F^internal

µ r=F^internal

where:

r: is the related coordinate (r₂-r₁)
µ: is the recipical of m₁+m₂=m₁m₂/m₁+m₂ which is the reduced mass

r is the relative serperation
eg for a spring F^internal=-kx Þ µ x=-kx
SHM with angular frequency w ₀²=k/µ=k/m₁m₂(m₁+m₂) this can be used to calculate the ratio of the natural frequencies of H₂ and HCl

4.1 One Dimensional Collisions

2 particles only
internal force acts for a very short time
physical interaction is not essential, for example Coulomb Repulsion

Choose a frame in which:

particles approach to each other is along a stationary straight line
x-axis is a line to this (along) line

We define a one dimensional collision as a collision that takes place along a line and they seperate along the line.

m₁x₁=-F^internal

m₂x₂=+F^internal

m₁x₁+m₂x₂=constant

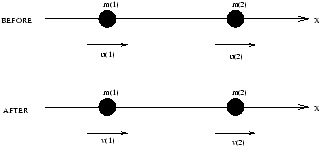
m₁u₁+m₂u₂=m₁v₁+m₂v₂

If F^internal is a conservative force, then the total energy in the system is conserved

E=K+U

Hard collisions are examples of many collisions where U acts over a short range (eg billiard balls) so that (except for the short contact time)

K_initial=K_final

in which case

m₁u₁²+

u₂u₂²=

m₁v₁²+

m₂v₂²

this is know as an Elastic Collision.

When given the initial velocities (u₁, u₂) calculate the final velocities (v₁, v₂) consider kinetic energy ® m₁(v₁²-u₁²)=m₂(u₂²-v₂²)
consider the momentum ® m₁(v₁-u₁)=m₂(u₂-v₂)

NOTE: (A₁²-B₁²)=(A₁-B₁)(A₁+B₁)

by dividing:

v₁+u₁=v₂+u₂

v₁-v₂=-(u₁-u₂)

We can now use this information to solve for v₁ and v₂

v₁=

2m₂u₂+(m₁-m₂)u₁

m₁+m₂

v₂=

2m₁u₁+(m₂-m₁)u₂

m₁+m₂

4.1.1 Special Case: Stationary Target

u₂=0

v₁=

m₁-m₂

m₁+m₂

v₂=

2m₁u₁

m₁+m₂

If m₁=m₂ v₁=0 and v₂=u₁ so therefore 100% energy transfer

m₁>m₂ v₁>0 and v₂>0

m₁<m₂ v₁<0 and v₂>0

m₁« m₂ v₁=-u₁ and v₂=0 (brick wall rebound)

4.1.2 Special Case: Equal but Opposite Initial Velocities

At what velocity does the lighter mass recoil when u₁=-u₂ ?

v₂=

2m₁u+(m₂-m₂)(-u)

m₁+m₂

æ
ç
ç
è

3m₁-m₂

m₁+m₂

ö
÷
÷
ø

v₂=

æ
ç
ç
è

3r -1

r +1

ö
÷
÷
ø

where r =m₁/m₂

m₁» m₂ v₂=3u

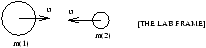
4.1.3 Centre of Mass Frame

The centre of mass frame is a frame in which the coordinates of the partile are measured relative to the centre of mass.

Centre of mass coordinates: r₁^*=r₁-R and r₂^*=r₂-R

m₁r₁-m₂r₂

m₁+m₂

where R is the position of the centre of mass
velocity of mass m₁ in the centre of mass frame

r₁^*=r₁-R

V₁^*=v₁-V

Example

Two bodies collide ellastically with equal and opposite velocity u and -u . Show that the lighter mass cannot recoil with speed greater than 3u .

V~ u

Þ u₁^*=u₁-V=u-u=0

Þ u₂^*=u₂-V=-u-u=-2u

In the centre of mass frame we have a brickwall rebound.

ie v₂^*=+2u

Transform this back to the lab frame

v₂=v₂^*+V=+2u+u=3u

4.1.4 Inelastic Collisions

Kinetic energy is now no longer conserved

K_f<K_i

Coefficient of Restitution

v₂-v₁=(u₁-u₂)e

where 0³ e£ 1 , if e=1 then collision is totally elastic, however if e=0 then the collision is totally inelastic (putty like).
Combine this with the conservation of momentum equation and solve for v₁ and v₂

v₁=

m₁u₁+m₂[u₂+e(u₂-u₁)]

m₁+m₂

v₂=

m₂u₂+m₁[u₁+e(u₁-u₂)]

m₁+m₂

for an equal approach collision

v₂=

æ
ç
ç
è

(2e+1)m₁-m₂

m₁+m₂

ö
÷
÷
ø

æ
ç
ç
è

(2e+1)r -1

r +1

ö
÷
÷
ø

as r ® big number, v₂ ® (2e+1)u

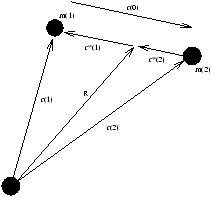
4.2 Center of Mass Frame (in general)

r=r₂-r₁

m₁r₁+m₂r₂

m₁+m₂

Solve for r₁ and r₂ in terms of R and r

MR=m₁r₁+m₂r₂

m₂r=m₂r₂-m₂r₁

MR=m₂r=(m₁+m₂)r₁

r₁=R-

m₂

r₂=R+

m₁

4.2.1 Momentum in a Centre of Mass Frame

The position of the mass m₁ in the centre of mass frame is r₁^*=r₁-R
The momentum in the in the centre of mass frame for the mass m₁

m₁r₁^*=m₁(r₁+R₁)

by using the general equations of centre of mass

m₁r₁^*=p₁^*=-

m₁m₂

.r=-µ dotr

p₂^*=m₂r₂^*=µ r

Total momentum p₁^*+p₂^*=0 . In a centre of mass frame the total momentum of the system disappears.

4.2.2 Kinetic Energy in a Centre of Mass Frame

for mass 1:

K₁^*=

m₁|r₁^*|²=

|p₁^*|²

m₁

µ ²|r|²

2m₁

for mass 2:

K₂^*=

m₂|r₂^*|²=

|p₂^*|²

m₂

µ ²|r|²

2m₂

so the total kinetic energy in a centre of mass frame

K^*=K₁^*+K₂^*=

(

m₁

m₂

)|r|²µ ²=

µ ^-1|r|²µ ²=

µ |r|²

relating the centre of mass kinetic energy to the lab frame kinetic energy

K=K_CoM+K^*=

M|R|²+

µ |r²

what is K_CoM equal to, we don't know.

Working in one dimension:

r ® x₁

r₁ ® x₁ etc ...

r ® x º x₂-x₁

x₁=X-

m₂

x₂=X+

m₁

same for velocities:

x₁=X-

m₂

x₂=X-

m₁

The lab kinetic energy:

m₁x₁²+

m₂x₂²=

m₁(X-

m²

x)²+

m₂(X+

m₁

x)²=

(m₁+m₂)X²-

m₁m₂

xX+

m₁m₂

Xx+

m₁

æ
ç
ç
è

m₂

ö
÷
÷
ø

x²+

m₂

æ
ç
ç
è

m₁

ö
÷
÷
ø

x²

[

m₁

× µ ²+

m₂

× µ ²]x²=

[

m₁

m₂

]µ ²x²

however µ ^-1=1/m₁+1/m₂

MX²+

µ x²

4.2.3 Example

Calculate the change in kinetic energy for an inelastic one dimensional collision

Method 1: Lab Frame

K_before=

m₁u₁²+

m₂u₂²

K_after=

m₁v₁²+

m₂v₂²

D K=K_before-K_after=

m₁(u₁²-v₁²)+

m₂(u₂²-v₂²)

conserve momentum:

m₁u₁+m₂u₂=m₁v₁+m₂v₂

resititution:

v₂-v₁=e(u₁-u₂)

now solve simultaneously for v₁ and v₂ and then substitute into D K ¾® NASTY!!!!

Method 2: Centre of Mass Frame

K_before=K_CoM+K_before^*

K_after=K_CoM+K_after^*

D K=K_before^*-K_after^*

given K^*=1/2µ |r|²

K_before^*=

µ (u₁-u₂)²

K_after^*=

µ (v₁-v₂)²=

µ e²(u₁-u₂)²

D K=

µ (u₁-u₂)²(1-e²)=

æ
ç
ç
è

m₁m₂

m₁+m₂

ö
÷
÷
ø

(u₁-u₂)²(1-e²)

K_CoM=

MX²

but mX=constant and so K(CoM)_before=K(CoM)_after

4.3 Rocket Motion

Two Body - Rocket and Fuel. In an isolated system momentum is conserved, therefore constant; from Newton II we get

(mv)=

for a rocket in space F=0 however dv/dt¹ 0 so dm/dt¹ 0 in this case. Fuel is ejected from the rocket with velocity -V_ex relative to the rocket. Therefore the lab observer sees the exhast to move with velocity v-v_ex (cf Young and Freedman page 250, this reference has the exhaust arrow in the wrong direction). Momentum conserved:

p(t)=mv

p(t+dt)=(m+dm)(v+dv)-dm(v-v_ex)=mv+mdv+vdm+(dmdv)-vdm+v_exdm

we ignore (dmdv) as it is second order and so very small.

mv=mv+mdv+v_exdm

mdv=-v_exdm

If we divide by dt then this expression has the dimensions of force, the thrust of the system

=-v_ex

rearranging:

ó
õ

m_f

m_i

ó
õ

v_f

v_i

v_ex

however v_ex is a constant

æ
ç
ç
è

m_f

m_i

ö
÷
÷
ø

v_ex

(v_f-v_i)

but ln X=-ln 1/X

æ
ç
ç
è

m_i

m_f

ö
÷
÷
ø

v_ex

(v_f-v_i)

m_i=m_fe

v_f-v_i

v_ex

m_f=m_ie

v_f-v_i

v_ex

the initial fuel mass (m_i-m_f)

speed boost (v_f-v_i) depends on v_ex but is independent of the burn rate ( dm/dt )
in practive v_ex£ 4kms^-1 for chemical based rockets, this is about the limit for chemical rockets
v_f can exceed v_ex

4.3.1 Rockets in the Presence of Gravity - Launch Vechicles

Assume gravity doesn't vary with height by Newton II

F_ext=-mg

lim

dt 0

[

P(t+dt)-P(t)

]=-mg

lim

dt 0

[

(m+dm)(v+dv)-dm(v-v_ex)-mv

]=-mg

+v_ex

=-mg

-v_ex

-g

ó
õ

v_f

v_i

dv=-v_ex

ó
õ

m_f

m_i

-g

ó
õ

v_f-v_i=-v_ex.ln

æ
ç
ç
è

m_f

m_i

ö
÷
÷
ø

-gt

v_f-v_i=v_ex.ln

æ
ç
ç
è

m_i

m_f

ö
÷
÷
ø

-gt

For dv/dt>0 requires v_ex|dm/dt|>gm

Thrust>Weight