Chapter 5 Introduction

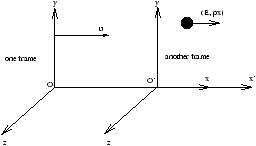
Mechanics when v~ c
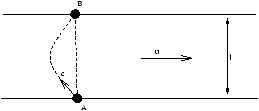
eg if a body moves to the right with velocity v' in a frame moving with velocity u then the lab observer will see the body move with velocity v

v'+u

uv'

c²

note that this reduces to v=v'+u when uv'« c

Issues

what do we mean by an observer
how do we give inertial observers a measure seperation in space and time
how are measurements of one inertial frame related to those of another

5.1 Postulates of Relativity

5.1.1 First Postulate

Galilean Relativity states that mechanical experiments cannot distinguish between inertial frames
Newton I states where no external forces are acting bodies move with constant velocity
however the Lows of Mechanics are covariant with respect to translating between different frames. Other quantities (eg charge, number of particles, [mass]) take the same value in each inertial frame - invariant.

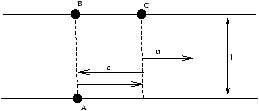
Can EM Experiments Distinguish Between Inertial Frames?

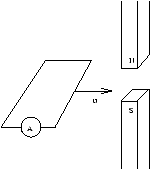
moving coil in a magnetic field
the charges in the wire feel a force and so a current flows
current pulse

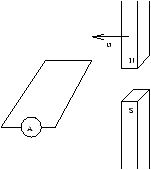
moving field over a coil
an induced emf where vµ -d/dtBA
current pulse

No it can't as the current pulse in both cases are identical regardless of the fact the experiment conditions are different. It turns out that all physical phenomena are like this. Einstein elevated this idea to a fundemental principle.

The Laws of Physics are the same for all Inertial frames/observers

The Michaelson and Morely Experiment (1887)

Suppose the earth moves in the frame of fixed stars within which resides an ether substance to support light waves, the earth fuels the ether wind. Consider the time taken for two round trips

CROSS-STREAM

resultant velocity =c²-u² so the time taken for a round trip

t

^
=

2l

c²-u²
ALONG STREAM

resultant velocity =c± u so the time taken for a round trip

t

=

l

c+u
+

l

c-u
=

2lc

c²-u²

Ratio: t/t_^=c/c²-u²=1/1-u²/c²=g
t >t_^ ie along stream journey takes longer than the cross stream journey.

c: =3×10⁸ms^-1
u: =3×10⁴ms^-1
l: =22m
t: =146.6666681ns
t_^: =146.6666674ns

=1+

D t

=1+10^-8

Using interferometric methods Michaelson and Morely could detect

cD t

Michaelson and Morely used l =589nm

589× 10^-9

22× 20

D t

=1.3× 10^-9

No detectable time difference in the Michaelson and Morely experiment and so in a given inertial frame c is the same in all direction, ie c is isotropic.

Further experiments (Kennedy-Thorndike experiment) also showed that the numerical value is the same in all inertial frames.

c=2.99792485× 10⁸ms^-1

Indeed from electromagnetic theory

e ₀µ ₀

where:

e ₀: =permittivity of free space
µ ₀: =permability of free space

e ₀ and µ ₀ are fundemental constants and so c must be a fundemental constant

5.1.2 Second Postulate

The speed of light is the same in all inertial frames, ie. invariant

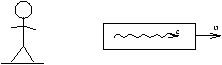
Light pulse on a train

No matter what u is, the platform observer measures speed of light on the train to be c (c+u=c)

5.2 Inertial Observers in Relativity

Inertial Free particles move in straight lines, covering equal distance in equal time

fill frame with latticework of rods and clocks
synchronise clocks. have a clock at position (x,y) read time t=x²+y²/c . start clock at origin and send out spherical light pulse. start clock at (x,y) when pulse reaches (x,y)

Observer means the lattic work of rods and clocks recording events in the inertial frame

5.3 Transverse Spatial Separation

We want to compare measurements of space and time seperation of one inertial observer with another.

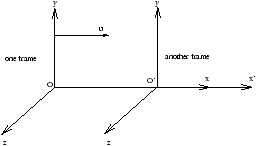
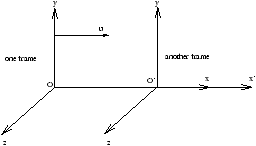
Choose our Standard Orientation

O' places 1m ruler along his y-axis and compares its length with O 's ruleras they pass each other at t=t'=0 Answer it must be 1m by principle of relativity, so for transverse distances y'=y and z'=z. Distances transverve to direction of relative motion between frames are invariant.

5.4 Lesson's from a Light Clock

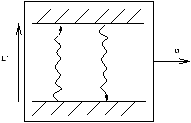
Start in rocket frame O'

Mirror serperation L' , events:

light pulse leaves the lower mirror
light pulse is received at the upper mirrow
light pulse returns to the lower mirrow

These three events make up the period of our clock

2L'=ct

period=t

However in a stationary frame this is observed

Time for one tick=t/2
Distance moved by the rocket during one tick=ut/2
Distance traveled by the light pulse during one tick=ct/2
Perpendicular distance:

L=[

æ
ç
ç
è

ö
÷
÷
ø

æ
ç
ç
è

ö
÷
÷
ø

]

c²-u²

However transverse distances are invariant so L'=L

c²-u²=t g

where:

g: ³ 1
t: >t

however there is trouble for u>c as we get the equation to become complex.

This principle occurs for all processes (biological, mechanical, atomic, etc) occurning at the same location.

In the rocket frame, the clock goes slower with respect to the lab frame.

5.4.1 Proper Time

In general the time seperation between events occuring at the same place in a given frame is called the proper time.

Here t is the proper time between events 1 and 3. t is the time recorded between events 1 and 3 in a frame where they occur at the same place.

Decay of Muons in the Atmosphere

In the lab a box of muons will decay according to

N(t)=N(0)e

2.2

where t is in microseconds (µ s)

Muons are produced at a height of 2km and travel at u=0.995c . Therefore the time to reach the ground is 2× 10³/0.995× (3× 10⁸)=6.7µ s . Therefore we expect N(t)/N0=e^-^6.7/2.2= 5% remain. However what we observe is around 70%.

This is caused by the lifetime of the muon being actually g times longer in the lab frame than in the rest frame of muon 2.2µ s ¾® (g × 2.2µ s).

g =

1-0.995²

~ 10

N(t)

6.7

2.2

~ 70%

5.5 Interval Invariance

Light clock in hyper-rocket frame

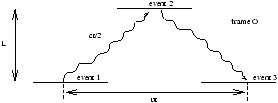
Lab frame moves at a speed -u relative to the rocket frame.

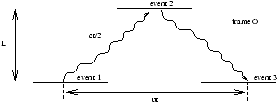
Hyper-rocket frame moves at a speed u to right relative to rocket frame.

Introduce a third frame O'(hyper-rocket frame) moving at speed u relative to O' and analyse space-time coordinates of events 1,2 and 3 for all three frames.

t: thime seperation between 1 and 3 in lab
t: time seperation between 1 and 3 in rocket
t'': time seperation between 1 and 3 in O''
x: space seperation between 1 and 3 in lab
x'=0: space seperation between 1 and 3 in rocket
x'': space seperation between 1 and 3 in O''

Now L=L'=L'' and therefore O=O'=O''

[c²

æ
ç
ç
è

ö
÷
÷
ø

æ
ç
ç
è

ö
÷
÷
ø

]

=[c²

æ
ç
ç
è

t''

ö
÷
÷
ø

æ
ç
ç
è

x''

ö
÷
÷
ø

]

ie the quantity (ct)²-x²º (interval)² and is an invariant between frames. Note however using standard orientation where (t,x) measure space-time seperation with respect to reference event when the origins co-incide (the reference event at t=0). (interval)² can be positive, zero or negative, similar to pythagorus in euclidian geometry however complex solutions do exist. If negative we define

(interval)²=c²t²-x²=c²t ²=negative

then

(ct )²=-(s)²=x²-c²t²

and so is more spacelike rather than timelike.

Generalise to three spatial coordinates

c²t²-x²-y²-z²=c²t'²-x'²-x'²-z'² etc...

5.6 Relativity of Simultanity

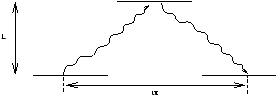
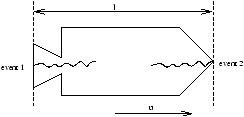
Set origin at rear of rocket standard orientation. Light pulses emitted fram each end simultaneously in lab frame.

Event 1: Lab t₁=0, x₁=0 ; Rocket t'₁=0, x'₁=0
Event 2: Lab t₂=0, x₂=l ; Rocket t'₂=?, x'₂=l₀
where:

l: is the length of the rocket for the lab
l₀: is the length of the rocket for the rocket

lab view of experiment (light pulses are emitted simultaneously t=0)

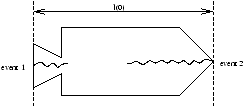
rocket view of experiment

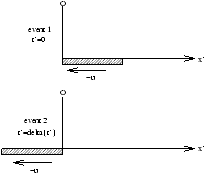
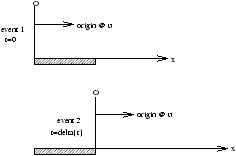
Pulses meet at some point to the left of the mid-point of the rocket (since the rocket moves to the right) therefore event 2 occurs before event 1, ie t'₂<0 . When origins coincide, lab observer sees rocket clocks along positive x-axis as

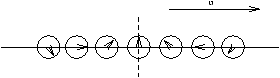
labs view of rocket clocks at t=0

Here we conclude if two events occur simultaneously in one frame they don't in another frame.

5.7 Relativity of Length

Place a ruler along the x-axis in the lab frame. The length in the lab frame is equal to l₀

How to measure the length in the rocket frame? The rocket sees the ruler approach with speed -u and take D t' to pass through the origin of the lab. so l (length for rocket)=uD t' . Lab sees the rocket origin approach with speed +u and takes time D t to pass through the rocket origin. So the length measured by the lab observer is l₀=uD t , however D t=g D t'

l_o

=l₀

v²

c²

therefore the ruler appears shorter in the rocket frame.

Lab View:

Rocket View:

5.8 Lorentz Transformations

Start with O and O' in standard orientation, where fames coincide at t=t'=0

Suppose some event occurs at (t, x, y, z) in frame O and at (t', x', y', z') in frame O' .

Then these make up the Lorentz transformations for O ® O'

t'=g (t-

c²

)

x'=g (x-ut)

y'=y

z'=z

These equations make up the Lorentz tranformations for O' ® O

t=g (t'+

ux'

c²

)

x=g (x'+ut')

y=y'

z=z'

Assume relationship between (x', t' ) and (x, t) is linear

x'=Ax+B(ct)

t'=D

æ
ç
ç
è

ö
÷
÷
ø

+Et

A, B, D, E are constants to be determined

æ
ç
ç
è

ö
÷
÷
ø

+cB

æ
ç
ç
è

ö
÷
÷
ø

5.8.1 Steps to Obtain the Lorentz Transformations

light pulse propagates in positive x direction. the speed is +c in both frames

c=

Ac+Bc

Dc

c
+E

1=

A+B

D+E
light pulse going in the -x direction

x'

t'
=-c,

x

t
=-c

-c=

A(-c)+cB

D

C
(-c)+E

1=

A-B

D-E
origin of O moves at velocity -u with respect to origin of O'

-u=

cB

E

we can combine (1), (2) and (3) to show

E=A, B=D=- æ
ç
ç
è

u

c
ö
÷
÷
ø A
obtained from (1)± (2)
interval invariance
(ct')²-(x')²=(ct)²-x²

c²[D æ
ç
ç
è

x

c
ö
÷
÷
ø +Et]²-[Ax+B(ct)]²º (ct)²-x²
as true for all values of x and t it is an identity (hence the º )
x² D²-A²=-1
however D=-( u/c) A

u²

c²
A²-A²=-1

A²(

u²

c²
-1)=-1

A=

1

1-

u²

c²

=g
therefore we can derive the Lorentz transformations

5.8.2 Special Cases

Light Clock Time Dialation
x'=0 t=g t
Relativity of Simultaneity
t=0, x¹ 0

t'=

-g ux

c²
Contraction of Length
x=l₀, t'=0, x'=l

l₀=g l

l=

l₀

g

N.B. for two general events (1)=(t₁, x₁) and (2)=(t₂, x₂) the Lorentz transformation is

D x'=g (D x-uD t)

where:

D x'=x'₂-x'₁

D x=x₂-x₁

D t=t₂-t₁

etc

For u« c where g ~ 1 the Lorentz transformations

x'=x-ut

t'=t-

c²

therefore even at low speeds t'¹ t provided x is large enough

5.9 Velocity Addition

v'=

dx'

dt'

g (dx-udt)

g (dt-u

c²

)

-u

c²

æ
ç
ç
è

ö
÷
÷
ø

however

=v Þ v'=

v-u

c²

Þ v=

v'+u

uv'

c²

Note:

for v' , u« c we have
v=v'+u
for v'=c

v=

c+u

1+

uc

c²

=c[

c+u

c+u
]=c

5.9.1 Example

An object moves with velocity 0.8c in a frame which moves with velocity 0.5c relating to another frame. What is the velocity of the object in the object in the the other frame.

v'=0.8c; u=0.5c v=

0.8c+0.5c

0.8c× 0.5c

c²

=0.93c

N.B. for two particles in a single frame

In the lab frame particle 1 moves at speed c with respect to particle 2. However this is a geometrical relative velocity and no particle is travelling at c in a particle frame.

5.10 Relativistic Momentum and Energy

Classically P=mv , if v<c then classically momentum is limited. However at high speed collisions indicate that the quantity mv is not conserved. Either

(a): we abandon momentum conservation
(b): modify its definition so that we reproduce Newtonian limit for v« c .

Consider two events with spacetime seperation (D t, D x) in the lab frame and (D t , 0)

cD t =[c²D t²-D x²]

we know that this quantity is invariant.

Divide by another invariant quantity: D t/m

m: =mass of particle deisplaced in spacetime by (D t, D x) . m is invariant

mc=[

æ
ç
ç
è

D t

ö
÷
÷
ø

æ
ç
ç
è

D x

D t

ö
÷
÷
ø

]

=[F²-Q²]

But D t=g D t

cD t =[c²D t²-D x²]

=cD t[1-

æ
ç
ç
è

D x

D t

ö
÷
÷
ø

]

D t=g D t =

D t

v²

c²

So F and Q become

F=g mc; Q=g mv

Q=g mv=

v²

c²

Low v limit v« c

Q~ mv[1+

v²

2c²

+...]

Experiments show that the value of Q summed over all particles in an isolated system is conserved, therefore relativistic expression for the momentum of a particle moving with speed v is: p=g mv=mv/1+v²/c²

5.11 Conclusion to Relativity

E=g mc²

P=g mv; v=

g =

v²

c²

What is E', p_x' in frame O'

E'=g 'mc²

g '=

v'²

c'²

p_x=g 'mv'

v'=

dx'

dt'

Application - Doppler effect see the handout