


Chapter 5 Thermodynamic Potentials
5.1 The Potentials - See Handout
5.2 Helmholtz Free Energy
F=U-TS is related to the maximum amount of extractable work in any given system.
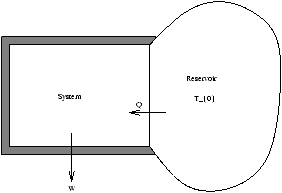
Figure 5.1 - System Converting Heat into Work
Let the system perform work W drawing heat Q from the reservoir. The system has the initial and final temperature T0 (but may have T T0 in between).
The total entropy satisfies
D S+D S0³ 0
where S is the system and S0 is the reservoir
Q-T0D S£ 0
The first law says D U=Q-W so we can now eliminate Q
Þ D U+W-T0D S£ 0
D (U-T0S)+W£ 0
however F=U-TS so
D F+W£ 0
W£ -D F (5.1)
For a process with Ti=Tf=T0 the maximum work the system can do which equals the decrease in F .
ie. -D F is the work freed by the process
If no work is done, then
D F£ 0 (5.2)
F never increases and is minimized at equilibrium (we recall that for a thermally isolated system D S³ 0 and dS=0 at equilibrium).
So the Minimum Principle of F for a mechanically isolated system, D F£ 0 (if Ti=Tf ), and F is a minimum at equilibrium. Some points about this though are
-
the condition on F refers to the system only
- the direction of process is D F£ 0
- the equilibrium condition is dF=0
So the explicit solutions for F is:
| P= |
æ
ç
ç
è |
|
ö
÷
÷
ø |
|
, S=- |
æ
ç
ç
è |
|
ö
÷
÷
ø |
|
| S=NlnV+ |
|
NklnT+S0 (for an ideal gas) |
|
F= |
|
NkT- |
|
NTlnT-NkTlnV-S0T=-NkTlnV+f(T) (5.3) |
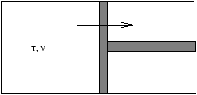
Figure 5.2 - An Example of
F
The gas in a cylinder and reservoir temp T where the expansion V1® V2
| D F=F2-F!=-NTlnV2+NkTlnV1=-NkTln |
|
W£ Wmax=-D F
this is equal to the work done by a quasistatic isothermal expansion process.
5.3 Chemical Potential - Changing N
There are many situations in which N varies, eg. in chemical reactions, phase transistions such as pourous containers so now
dU¹ TdS-PdV
as U=U(S,V,N) so we use
dU=TdS-PdV+µ dN
µ is the chemical potential
If U=U(S,V,N1,N2,N3,... ) then
this is made more natural in terms of
G=U+PV-TS
dG=VdP-SdT+µ dN
but G(P,T,N)=Ng(P,T) so
µ =g(P,T)
which is the specific Gibbs functions for one type of particle
dG=gdN+Ndg
dG=VdP-SdT+µ dN
Þ Ndg=VdP-SdT
we now let v=V/N and s=S/N so we obtain
dg=vdP-sdT
and we recall that
G=NkTlnP+N× (function of T)
µ =kTlnP+f(T) (5.5)
this is the equilibrium condidtion on µ
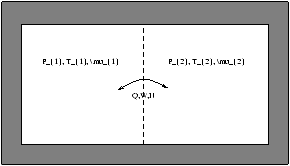
Figure 5.3 - Pourous Partition
The equilibrium conditions are dS=dS1+dS2=0 , dU1+dU2=0 , dV1+dV2=0 and dN1+dN2=0 . The fundenmental equation for dS1 and dS2 si
| |
|
(dU1+P1dV1-µ1dN1)+ |
|
(dU2+P2dV2-µ2dN2)=0 |
(something)dU1+(something)dV1+(something)dN1=0
Þ T1=T2, P1=P2, µ1=µ2
see also section 4.5
5.3.1 Example - A Gas in a Gravitational Field
How does P vary with the height z at a given T
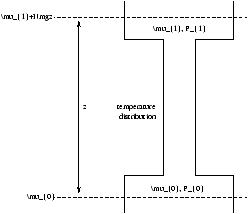
Figure 5.4 - Gravitational Effects on a Gas
µ0=kTlnP0+f(T)
µ1=kTlnP1+f(T)+mgz
the condition of equilibrium is µ0=µ1 so
kTlnP0=kTlnP1+mgz
5.4 Phase Equilibrium
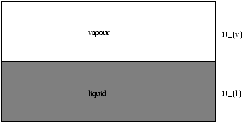
Figure 5.5 - Phase Equilibria (at constant
P and
T )
we seek a curve in the PT plane
G=Nlgl+Nvgv
N=Nl+Nv=constant
the equilibrium condition is dG=0
Þ gl(T,P)=gv(T,P)
this is true along the curve at ( T, P ). ie. also at ( T+dT, P+dP )
Þ dgl=dgv
we recall that dg=vdP-sdT so
vldP-sldT=vvdP-svdT
(sv-sl)dT=(vv-vl)dP
we now let l=T(sv-sl) which is the latent heat of evapouration (per particle)
this is the Clausius Clapeyon Equation.
However if vv>>vl we can use PV=NkT instead so that P=kT/V can be solved
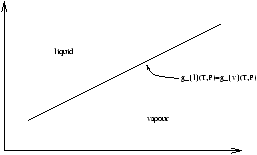
Figure 5.6 - Calculating
P=
kT/
V
5.5 The Third Law
What happens to S as T® 0 ? The physical order increases as T® 0 .
D S may be measured, it was Nerrist in 1906 who noted that D S® 0 as T® 0 in many reactions.
So we may choose S® 0 as T® 0
S(T,x)® 0 as T® 0 (for all x) (5.7)
where x=P or x=V , etc. This is the Third Law. eg. an ideal gas S~lnT . lnT® -¥ as T® 0 , hence the ideal gas behaviour cannot hold as T® 0 .
For paramagnetic systems
so Curie's Law M~B/T must fail as T® 0
S(T,P)® 0 as T® 0
Þ CP(T)® 0 (faster than T)
for example when CP is a constant S® -¥ . For metals CP=aT+bT3 whilst for other solids is is generally CP=aT3 . Also we let the expansitivity ( b ) by
| b = |
|
æ
ç
ç
è |
|
ö
÷
÷
ø |
|
=- |
|
æ
ç
ç
è |
|
ö
÷
÷
ø |
|
(Maxwell Relation) |
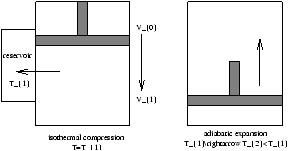
Figure 5.7 - ??
we use cool gas as a reservoir for another cyclinder and repeat many times
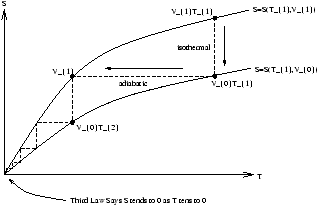
Figure 5.8 - ??
because S(T,V0) and S(T,V1) are convergeal at T=0 , so we need an infinite number of steps to reach T=0 .

















