Previous Contents Next

Chapter 4   The Fundemental Law

4.1   Combined First and Second Laws

dU=d-6mu'26 Q-d-6mu'26 W
d-6mu'26£ TdS
or for a reversible process
d-6mu'26 =TdS

d-6mu'26 W£ PdV
or for a reversible process
d-6mu'26 W=PdV

For reversible processes we therefore have
dU=TdS-PdV     (4.1)
This is the fundamental equation of thermodynamics

However this equation now depends on state functions only (so there is no Q or W ). It describes the relationship between state variables at neighbouring equilibrium points. So it is independent of whether we move between those points by a reversible or irreversible process.

4.2   Mathematical Structure

dU=TdS-PdV
U=U(S,V)
Þ dU= æ
ç
ç
è
U
S
ö
÷
÷
ø
 



V
dS+ æ
ç
ç
è
U
V
ö
÷
÷
ø
 



S
dV
by comparing to the previous equations
T= æ
ç
ç
è
U
S
ö
÷
÷
ø
 



V
,  P=- æ
ç
ç
è
U
V
ö
÷
÷
ø
 



S
æ
ç
ç
è
T
V
ö
÷
÷
ø		 =
2U
V S
=
2U
S V
=- æ
ç
ç
è
P
S
ö
÷
÷
ø
 



V
æ
ç
ç
è
T
V
ö
÷
÷
ø		 =- æ
ç
ç
è
P
S
ö
÷
÷
ø
 



V
    (4.2)
This is an Example of a Maxwell relation (relations between partial derivatives).

4.2.1   An Example

dS=
1
T
dU+
P
T
dV
S=S(U,V)
æ
ç
ç
è
S
U
ö
÷
÷
ø
 



V
=
1
T
,   æ
ç
ç
è
S
V
ö
÷
÷
ø
 



U
=
P
T
Þ
V
æ
ç
ç
è
1
T
ö
÷
÷
ø
 



U
=
U
æ
ç
ç
è
P
T
ö
÷
÷
ø
 



V
Check for ideal gas using U=cVT and PV=NkT .

4.3   Internal Energy

Given the equation of state (eg. Van der Waal's) what can we say about U(T,V)?
dU=TdS-PdV
we want U=U(T,V) so let S=S(T,V)
Þ dS= æ
ç
ç
è
S
T
ö
÷
÷
ø
 



V
dT+ æ
ç
ç
è
S
V
ö
÷
÷
ø
 



T
dV

dU=T æ
ç
ç
è
S
T
ö
÷
÷
ø
 



V
dT+ é
ê
ê
ê
ê
ê
ë		 T æ
ç
ç
è
S
V
ö
÷
÷
ø
 



T
-P ù
ú
ú
ú
ú
ú
û		 dV
also we have
dU= æ
ç
ç
è
U
T
ö
÷
÷
ø
 



V
dT+ æ
ç
ç
è
U
V
ö
÷
÷
ø
 



T
dV
and by comparing
æ
ç
ç
è
U
T
ö
÷
÷
ø
 



V
=T æ
ç
ç
è
S
T
ö
÷
÷
ø
 



V
    (4.3)
æ
ç
ç
è
U
V
ö
÷
÷
ø
 



T
=T æ
ç
ç
è
S
V
ö
÷
÷
ø
 



T
-P     (4.4)

V
(equation 4.3)=
T
(equation 4.4)
T
2S
V T
= æ
ç
ç
è
S
V
ö
÷
÷
ø
 



T
+T
2S
T V
- æ
ç
ç
è
P
T
ö
÷
÷
ø
 



V
æ
ç
ç
è
S
V
ö
÷
÷
ø
 



T
= æ
ç
ç
è
P
T
ö
÷
÷
ø
 



V
we now insert this into equation 4.4
æ
ç
ç
è
U
V
ö
÷
÷
ø
 



T
=T æ
ç
ç
è
P
T
ö
÷
÷
ø
 



V
-P     (4.5)
The right hand side depends only on T and V (since the equation of state gives P=P(T,V) ). Then equation 4.5 gives V dependence of U(T,V) . Equation 4.5 is therefore called the energy equation.

4.3.1   An Ideal Gas

P=NkT/V so equation 4.5 gives
æ
ç
ç
è
P
T
ö
÷
÷
ø
 



V
=
Nk
V
Þ æ
ç
ç
è
U
V
ö
÷
÷
ø
 



T
=T
Nk
V
-
NkT
V
=0
therefore as expected U=U(T) .

4.3.2   A Van der Waals Gas

æ
ç
ç
è		 P+a
N2
V2
ö
÷
÷
ø		 (V-Nb)=NkT
Þ æ
ç
ç
è
P
T
ö
÷
÷
ø
 



V
(V-Nb)=Nk
Þ æ
ç
ç
è
P
T
ö
÷
÷
ø
 



V
=
Nk
(V-Nb)
now we insert into equation 4.5
æ
ç
ç
è
U
V
ö
÷
÷
ø
 



T
=T
Nk
(V-Nb)
-P=P+a
N2
V2
-P  (using the equation of state)
æ
ç
ç
è
U
V
ö
÷
÷
ø
 



T
=a
N2
V2
U(T,V)=-a
N2
V
+f(T)
f(T)=cVT is to agree with the ideal gas case when a=0
U(T,V)=cVT-a
N2
V
    (4.6)

4.3.3   An Application - Temperature Change in Free Expansion

V0® V1 in adiabatic free expansion and so there is no work done ( W ) or heat flow ( Q ) so
D U=0
however T may drop for a Van der Waal's gas.

Let T=T(V,U)
dT= æ
ç
ç
è
T
V
ö
÷
÷
ø
 



U
dV+ æ
ç
ç
è
T
U
ö
÷
÷
ø
 



V
dU
however as dU=0
Þ D T= ó
õ
V1


V0
æ
ç
ç
è
T
V
ö
÷
÷
ø
 



U
dV
µJ= æ
ç
ç
è
T
V
ö
÷
÷
ø
 



U
=Joule Coefficient
we recall from section 2.7 the cyclic rule
æ
ç
ç
è
T
V
ö
÷
÷
ø
 



U
æ
ç
ç
è
U
T
ö
÷
÷
ø
 



V
æ
ç
ç
è
V
U
ö
÷
÷
ø
 



T
=-1
æ
ç
ç
è
T
V
ö
÷
÷
ø
 



U
=- æ
ç
ç
è
T
U
ö
÷
÷
ø
 



V
æ
ç
ç
è
U
V
ö
÷
÷
ø
 



T
=-
1
cv
æ
ç
ç
è
U
V
ö
÷
÷
ø
 



T
(cvdT=d-6mu'26 QV=dU)
or from using the energy equation we obtain
æ
ç
ç
è
T
V
ö
÷
÷
ø
 



U
=-
1
cv
é
ê
ê
ê
ê
ê
ë		 T æ
ç
ç
è
P
T
ö
÷
÷
ø
 



V
-P ù
ú
ú
ú
ú
ú
û
This is general so far. For a Van der Waal's gas
æ
ç
ç
è
U
V
ö
÷
÷
ø
 



T
=a
N2
V2
D T=- ó
õ
V1


V0
1
cv
a
N2
V2
d-6mu'26 V
D T=-
aN2
cv
é
ê
ê
ë		 -
1
V
ù
ú
ú
û
V1



V0
Þ D T=
aN2
cv
é
ê
ê
ë
1
V1
-
1
V0
ù
ú
ú
û		     (4.7)
This is usually less than zero since V1>V0 .

4.4   Entropy from the Fundamental Equation

The Fundamental Equation when rearranged says
dS=
dU
T
+
P
T
dV
so if we know U and P we may get S=S(T,V) . For an ideal gas U=3/2kT for the monotomic case and PV=NkT . We plug these values in an obtain
dS=
3
2
Nk
dT
T
+Nk
dV
V
Þ S=
3
2
NklnT+NklnV+constant
this can also be written as
S-S0=
3
2
Nkln
æ
ç
ç
è
T
T0
ö
÷
÷
ø
+Nkln
æ
ç
ç
è
V
V0
ö
÷
÷
ø
    (4.8)
along a reversible adiabats where dS=0
Nkln
æ
ç
ç
ç
è		 T
3
2
 
V ö
÷
÷
÷
ø
=constant
Þ T
3
2
 
V=constant
this is equivalent to PVg=constant .

For the case of a Van der Waal's gas where U=3/2NkT-aN2/V
dS=
1
T
æ
ç
ç
è
3
2
NkdT+a
N2
V2
dV ö
÷
÷
ø		 +
P
T
dV
we notice that
æ
ç
ç
è		 P+a
N2
V2
ö
÷
÷
ø		 =
NkT
(V-Nb)
dS=
3
2
Nk
dT
T
+Nk
dV
(V-Nb)
this is for the ideal gas where V® (V-Nb) .

S-S0=
3
2
Nkln
æ
ç
ç
è
T
T0
ö
÷
÷
ø
+Nkln
æ
ç
ç
è
V-Nb
V0-Nb
ö
÷
÷
ø
    (4.9)
The Entropy (in ??TD??) has no absolute meaning but we can compare entropy changes in Van der Waal's and the Ideal cases.
(D S)Van der Waals-(D S)ideal=Nkln
æ
ç
ç
è
V-Nb
V0-Nb
ö
÷
÷
ø
-Nkln
æ
ç
ç
è
V
V0
ö
÷
÷
ø
this is assuming that T=T0
(D S)Van der Waals-(D S)ideal=Nkln
æ
ç
ç
ç
ç
ç
è
1-
Nb
V
1-
Nb
V0
ö
÷
÷
÷
÷
÷
ø
therefore
V>V0Þ
1
V
<
1
V0
Þ -
1
V
>-
1
V0
(D S)Van der Waals>(D S)ideal  (if V>V0)


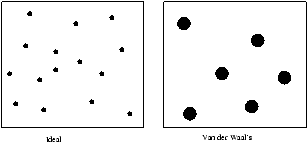
Figure 4.1 - Comparing the Ideal and Van der Waal Case
In the Van der Waal case the molcules occupy a finite volume b whilst in the ideal case the molecules are points. So in an expansion the molecules in the Van der Waal case experience a greater increase in freedom relative to the ideal case.
Þ (D S)Van der Waals>(D S)ideal

4.5   Entropy Max Principle


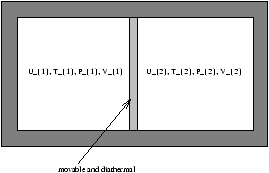
Figure 4.2 - ?????An Experiment?????
What are the equilibrium conditions? We use the Entropy Max Principle:

S=S1+S2 is maximized at equilibrium, subject to fixed U=U1+U2 and V=V1+V2 .

Therefore S is a maximum when dS=0
Þ dS1=-dS2
dU1
T1
+
P1
T1
dV1=- æ
ç
ç
è
dU2
T2
+
P2
T2
dV2 ö
÷
÷
ø
so when
dU=0Þ dU1=-dU2
dV=0Þ dV1=-dV2
so now the equilibrium condition is
dU1
T1
+
P1
T1
dV1=
dU1
T2
+
P2
T2
dV1
so U1 and V1 are independent variables
T1=T2,  P1=P2
so the Entropy Max Principle and the Fundamental Equation of ??TD?? gives us the equilibrium conditions.

4.6   Paramagnetism


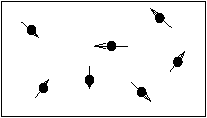
Figure 4.3 - A Box Full of Fixed Particles Each of Which is a Small Magnet

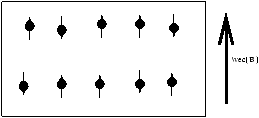
Figure 4.4 - The Box of Magnets Placed in a Magnetic Field
In the presence of a magnetic field the dipoles either align parallel or anti parallel to the magnetic field.
N=n1+n2 dipoles
where n1 is the number of dipoles aligned with B ( e1=-mB ) and n2 is the number of dipoles counter aligned with B ( e2=+mB ).

The total magnetism is
M=m(n1+n2)  (M=Nm at t=0)
Total Energy is
U=n1(-mB)+n2(+mB)
® U=-(n1-n2)mB=-MB
The Fundemental Equation (from Electricity and Magnetism first year)
dU=TdS-MdB
as M is extensive and B is intensive this means that B is like -P and M is like V . This is analogous to
d(U+PV)[=H]=TdS+VdP
so U=-MB is analogous to enthalpy H .

We also now need an equation of state
M=
cB
T
  (Curie's Law)
for some constant c at high temperatures.

From this we can tell that the isotherms are Mµ B and the adiabats are
dU=0-MdB
-d(UB)=-MdB
-dM.B-MdB=-MdB
Þ M=constant

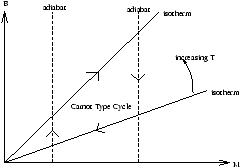
Figure 4.5 - Isotherms and Adiabats in Magnetism

4.6.1   Entropy

dS=
dU
T
+
MdB
T
=
d(-MB)
T
+
M
T
dB
Þ dS-
-B
T
dM=-
M
c
dM  (by Curie's Law)
Þ S=-
1
2c
M2+constant
This says that the entropy ( S ) decreases as M increases. So a high magnetism ( M ) gives high order and so a low value of S .

We can also derive the energy equation
Þ æ
ç
ç
è
U
B
ö
÷
÷
ø
 



T
=T æ
ç
ç
è
M
T
ö
÷
÷
ø
 



B
-M

4.7   A Preview of Statistical Mechanics

In Statistical Mechanics we look at the statistics of energy levels to get Thermodynamic information.

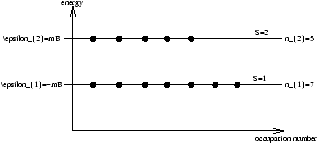
Figure 4.6 - The Model Used in Statistical Mechanics
What are the values of n1 and n2 at equilibrium at a temperature T ?

Statistical Mechanics tells us that the probability of being in level S is proportional to the Boltzmann Distribution.
µ e
-
eS
kT
 
Þ
nS
N
=
1
Z
e
eS
 
kT
for some constant Z , to fix Z we use
N=
2
å
S=1
nS=
N
Z
2
å
S=1
e
-
eS
kT
 
so we obtain Z=å e-eS/kT normalises the function, Z is called the Partition Function; so
Z=e
-
e1
kT
 
+e
-
e2
kT
 
Z=e
mB
kT
 
+e
-
mB
kT
 
Þ Z=2cosh
æ
ç
ç
è
mB
kT
ö
÷
÷
ø
we now compute M and the equation of state becomes
M=m(n1-n2)
M=m
N
Z
æ
ç
ç
ç
è		 e
mB
kT
 
+e
-
mB
kT
 
ö
÷
÷
÷
ø
M=mN×
2sinh
æ
ç
ç
è
mB
kT
ö
÷
÷
ø
2cosh
æ
ç
ç
è
mB
kT
ö
÷
÷
ø
Þ M=Nmtanh
æ
ç
ç
è
mB
kT
ö
÷
÷
ø
Thus the equation of state is
M~ Nm.
mB
kT
  (for large T)
tanhx~ x  (for small x)
M=
cB
T
Þ c=
Nm2
k
ie. this is as for Curie's Law (for high T ).

The values of n1 and n2 as T® 0 and T®¥
n1
N
=
e
mB
kT
 
2cosh
æ
ç
ç
è
mB
kT
ö
÷
÷
ø
n2
N
=
e
-mB
kT
 
2cosh
æ
ç
ç
è
mB
kT
ö
÷
÷
ø
 as T®¥ Þ n1®
1
2
 and n2®
1
2
 as T® 0 Þ n1® 1 and n2® 0
so as T®¥ ( kT>>mB ) there is an equal probability of the occupation of 1 or 2. However as T® 0 n1® N and n2® 0 , meaning that the highest probability is in the lowest state.

Previous Contents Next