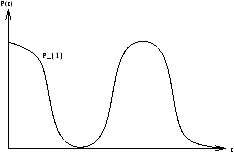
Figure 23.1 - The Nutation or Rabi Plopping



| t |
|
| Y (r | ,t)= |
|
cn(t)Un(r | )e |
|
(24.3) |
| Y (r,t)=c1(t)U1(r | )e |
|
+c2(t)U2(r | )e |
|
(24.6) |
|
Y (r,t)=(H0+V(t))Y (r,t) |
|
é ê ê ë |
E1c1(t)+ |
|
c1(t) |
ù ú ú û |
U1(r | )e |
|
+ |
é ê ê ë |
E2c2(t)+ |
|
c2(t) |
ù ú ú û |
U2(r | )e |
|
=c1(t) | [ | E1+V(t) | ] | U1(r | )e |
|
+c2(t) | [ | E2+V(t) | ] | U2(r | )e |
|
(24.7) |
| ó õ |
|
Um*UndV=dmn |
| ó õ |
|
Un*dV (24.8) |
| Un*=Un*(r | )e |
|
(24.9) |
|
c1(t)=c1(t) | ó õ |
|
U1*V | (t)U1dV+c2(t) | ó õ |
|
U1*V(t)U2dV |
|
c2(t)=c2(t) | ó õ |
|
U2*V | (t)U2dV+c1(t) | ó õ |
|
U2*V(t)U1dV (24.10) |
| ó õ |
|
Un*VUmdV (24.11) |
| w0= |
|
| c1(t)=cos |
|
c2(t)=-sin |
|
(24.16) |
| cos2 |
|
(24.17) |

| P(2)= |
|
g(E)|<2|U|1>|2t (24.18) |


