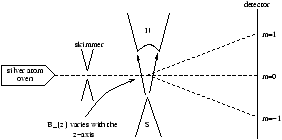
Figure 21.1 - Stern-Gerlach Experiment (1925)



| µ= |
|
.l (22.2) |
| Hint=- |
|
.BzLz (22.3) |
| µB= |
|
(22.5) |
| F=- |
|
V(z) |
| Fatom=µBm |
|
Bz(z) (22.6) |

| l= |
|
, m=± |
|
| S | 2c |
|
= |
|
2c |
|
(22.9) |
| Eint=-g |
|
msBz |
| c |
|
= |
æ ç ç è |
|
ö ÷ ÷ ø |
, c |
|
= |
æ ç ç è |
|
ö ÷ ÷ ø |
(22.10) |
| Sz= |
|
æ ç ç è |
|
ö ÷ ÷ ø |
= |
|
sz, Sy= |
|
æ ç ç è |
|
ö ÷ ÷ ø |
= |
|
sy, Sz= |
|
æ ç ç è |
|
ö ÷ ÷ ø |
= |
|
sx (22.11) |
| S2=Sx2+Sy2+Sz2= |
|
2 |
æ è |
|
ö ø |
(22.12) |
| S | zc |
|
= |
|
æ è |
|
ö ø |
æ ç ç è |
|
ö ÷ ÷ ø |
= |
|
æ è |
|
ö ø |
(22.13) |
| S | zc |
|
= |
|
2 |
æ ç ç è |
|
ö ÷ ÷ ø |
æ ç ç è |
|
ö ÷ ÷ ø |
= |
|
2 |
æ ç ç è |
|
ö ÷ ÷ ø |


