Previous Contents Next

Chapter 21   Lecture 20 - Angular Momentum in Atoms and Molecules

we recall that
L2Ylm(q ,f )=l(l+1)2Ylm(q ,f )

21.1   Diatomic Molecules

such as H2 , O2 , CO , HCl , etc

we can treat this as a rigid rotor where R is a constant

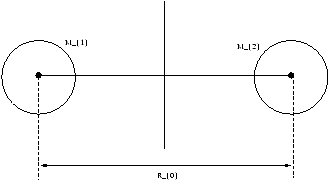
Figure 20.1 - Rotor Model
the moment of inertia about the centre of mass is
I=
m1m2
(m1+m2)
R02     (21.1)
classically the energy of rotation is
Erot=
L2
2I
    (21.2)
we can quantise this in the following way
Hrot=
1
2I
L2     (21.3)
Thus the rotational energy eigenstates are the eigenstates of L2
HrotYlm(q ,f )=
l(l+1)2
2I
Ylm(q ,f )
El=
2
2I
l(l+1)     (21.4)
so for example a O2 molecule
I=1.26× 10-46kgm2
  l=1Þ E1=5.7× 10-25J
  l=2Þ E2=1.7× 10-22J
the transistions between rotational states may occur, for example when l=1® 2 in an O2 molecule
D E=1.13× 10-22JÞn =1.7× 1011Hz
this is a frequency that lies in the far infrared or microwave region.

21.2   Central Potentials - Atoms

A central potential is spherically symmetric (definite parity)
V(r,q ,f )® V(r)
it reduces to a function in terms of only r , thus [P,H]=0 and also [P,L2]=[P,Lz]=0 .

The eigenstates of parity are also eigenstates of H , L2 and Lz . We wish to verifty that in this case H , L2 and Lz are compatible
H=
-2
2m
Ñ2+V(r)     (21.5)
we must use spherical polar for Ñ2
Ñ2º
2
r2
+
2
r
r
+
1
r2
æ
ç
ç
è
2
q2
+cotq
q
+
1
sinq
2
q2
ö
÷
÷
ø		     (21.6)
where
2
r2
+
2
r
r
ºPr2=[radial momentum]2
2
q2
+cotq
q
+
1
sinq
2
q2
º -
L2
2
=[angular momentum]2
we can rewrite H
H=
-2
2m
æ
ç
ç
è
2
r2
+
2
r
r
ö
÷
÷
ø		 +
L2
2mr2
+V(r)     (21.7)
where
-2
2m
æ
ç
ç
è
2
r2
+
2
r
r
ö
÷
÷
ø		 =radial kinetic energy  (µpr2)
L2
2mr2
=angular kinetic energy  (µL2)
V(r)=potential energy
[H,L2]=
-2
2m
[pr2,L2]+
1
2mr2
[L2,L2]+[V(r),L2]     (21.8)
where [L2,L2]=0 as they are compatible.

V(r) in a central potential depends only on r
[V(r),L2]=0
likewise because pr2 depends only on r
[pr2,L2]=0
[H,L2]=0     (21.9)
The energy and total angular momentum is compatible (also with Lz ).

Energy eigenstates are simultaneous eigenstates of L2 and Lz for a central point.

By using equation IV.50 we have
é
ê
ê
ë		 -
2
2m
æ
ç
ç
è
2
r2
+
2
r
r
ö
÷
÷
ø		 +
L2
2mr2
+V(r) ù
ú
ú
û		 Y (r,q ,f )=EY (r,q ,f )     (21.10)
The angular part of Y (r,q ,f ) must be the eigenstates of L2 , ie. sperical harmonics
Y (r,q ,f )=R(r)Ylm(q ,f )     (21.11)
we know that
L2R(r)Ylm(q ,f )=l(l+1)2R(r)Ylm(q ,f )     (21.12)
and so equation IV.53 can be simplified
é
ê
ê
ë		 -
2
2m
æ
ç
ç
è
d2
dr2
+
2
r
d
dr
-
l(l+1)
r2
ö
÷
÷
ø		 +V(r) ù
ú
ú
û		 R(r)=ER(r)     (21.13)
the properties of this are:
Previous Contents Next