Chapter 20 Lecture 19 - Eigenfunctions of Angular Momentum

20.1 Angular Momentum Eigenvalue Equation

We saw that

[L²,L_z]=[L²,L_x]=[L²,L_y]=0

thus eigenfunctions of L² cam be simultaneous eigenfunctions of L_z or L_x or L_y . By choosing L² and L_z (because the latter is especially convenient in spherical polars) we write

L²Y (r,q ,f )=a²Y (r,q ,f ) (20.1)

L_zY (r,q ,f )=bY (r,q ,f ) (20.2)

The operators L² and L_z are

L_z=-

¶q

L²=-

é
ê
ê
ë

¶²

¶q²

+cotq

¶q

sin²q

¶²

¶f²

ù
ú
ú
û

so these depend only on q and f since there is no r dependence we can write

Y (r,q ,f )=c (q )U(f )R(r) (20.3)

20.2 hat(L)z Eigenstates and Eigenvalues

From equations IV.25 and IV.26 we obtain

¶f

Y (f )=b U(f ) (20.4)

the solution is

U(f )=Ce

(20.5)

æ
ç
ç
ç
ç
è

ó
õ

|U(f )|²df =1Þ C=

ö
÷
÷
÷
÷
ø

Since the wavefunction U(f ) must be single valued we can deduce the boundary conditions.

U(f )=U(f +2p ) (20.6)

Þ e

This is satisified if

b =m (20.7)

this implies angular momentum is quantised where m is an integer. Therefore we obtain

U(f )=c (q )e

(20.8)

so in inserting this into equation IV.24 yields

-²

é
ê
ê
ë

¶²

¶q²

+cotq

¶q

sin²q

¶²

¶q²

ù
ú
ú
û

c (f )e

=a²c (f )e

(20.9)

so after performing the operation in f and rearranging

é
ê
ê
ë

d²

dq²

+cotq

m²

sin²q

a²

ù
ú
ú
û

c (q )=0 (20.10)

this is solved via the substitution x=cosq

é
ê
ê
ë

(1-x²)

d²

dx²

-2x

m²

1-x²

a²

ù
ú
ú
û

c (x)=0 (20.11)

This differential equation has a well known set of standard solutions

if m=0 then we have Legendre Polynominals
P₀(cosq)=1 [P_l(cosq)]

P₁(cosq)=cosq (20.12)
if m¹ 0 then we have Associated Legendre Polynominals
P_l⁰(cosq)=P_l(cosq) [P_l^m(cosq)]

P_l¹(cosq)=sinq (20.13)

but solutions only exist for discrete values of a²

a²=l(l+1)² (20.14)

where

l=0,1,2,... (integer) (20.15)

and is called the angular momentum quantum number for each l the permitted m values are

m=l,l-1,0,... ,-(l-1),-l (20.16)

note that

m_max =l <a -l(l+1)

This is essential to satisify uncertainity relations D L_zD L_x

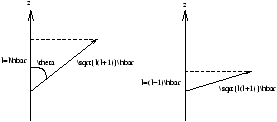
Figure 19.1 - A Heuristic Model

this shows that

the angle between l and quantisation axis z (known as angular quantised)
for m_max =a we need q =0 . If this was so L_x and L_y would be perfectly determined (ie. zero) as was L_z , because this would violate the uncertainity principle

20.3 Spherical Harmonics

The complete normalised angular momentum eigenfunctions are labelled Y_lm(q ,f ) called spherical harmonics.

Y_lm(q ,f )=(-1)^m

é
ê
ê
ë

(2l+1)(l-|m|)!

4p (l+|m|)!

ù
ú
ú
û

× P_l^|m|(cosq

(20.17)

the outcomes of this are:

a set of orthornormal functions
simultaneous eigenfunctions of L² and L_z and for a central potential also H
status have definite parity since
[P,L²]=[P,L_z]=0 (20.18)