Chapter 19 Lecture 18 - Operators for Angular Momentum and Their Commutation Relations

19.1 Angular Momentum Operator

In one dimension linear momentum is

p_x=-

¶ x

therefore in three dimensions linear momentum now becomes

p=-Ñ (19.1)

Ñ=i

¶ x

¶ y

¶ z

(19.2)

L=r×p=-(r×Ñ) (angular momentum) (19.3)

L_x=-

æ
ç
ç
è

¶ z

-z

¶ y

ö
÷
÷
ø

L_y=-

æ
ç
ç
è

¶ x

-x

¶ z

ö
÷
÷
ø

L_z=-

æ
ç
ç
è

¶ y

-y

¶ z

ö
÷
÷
ø

(19.4)

Note that this involves products like y and p_z , z and p_x , etc. For which there are no compatibility issues.

If they had terms such as y and p_y we would be in big trouble due to simultaneous measurement of incompatible quantities.

Equation IV.18 expressions can be generated from each other by applying a rule of cyclic permutation

x® y, y® z, z® x

L²=L_x²+L_y²+L_z² (19.5)

this is the total angular momentum squared. Often it will be most convenient to use spherical polars in this coordinate frame. We have the important ones

L_z=-

¶f

(19.6)

L²=-²

é
ê
ê
ë

¶²

¶q²

+cotq

¶q

sin²q

¶²

¶f²

ù
ú
ú
û

(19.7)

19.2 Compatibility of Angular Momentum Operators

The physical considerations in polars are

L_z=-

¶f

this has a close analogy to p_z=¶/¶ z we recall that there is an uncertainity relation

D zD p_z

so z and p_z are not compatible and so therefore we anticipate a similar uncertainity relation between f and -¶/¶f

DfD L_z

(19.8)

If L_z is perfectly defined ( D L_Z=0 ) this implies f must be completely uncertain (ie. has any value between 0 and 2p with equal probability).

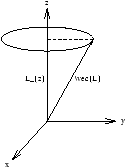
Figure 18.1 - Complete Uncertainity in f

f is undefined therefore the x and y components of L must also be undefined if L_z is defined. Therefore we say that L_z is incompatible with L_x and L_y .

19.3 Communtation Relations Between Angular Momentum Operators

[L_x,L_y]=²

é
ê
ê
ë

æ
ç
ç
è

¶ z

-z

¶ y

ö
÷
÷
ø

æ
ç
ç
è

¶ x

-x

¶ z

ö
÷
÷
ø

ù
ú
ú
û

this to calculate is grizzly but it can be multiplied out where terms cancel out.

[L_x,L_y]=-²

æ
ç
ç
è

¶ z

-z

¶ y

ö
÷
÷
ø

=²

æ
ç
ç
è

¶ y

-y

¶ x

ö
÷
÷
ø

a comparison to equation IV.18 shows

[L_x,L_y]=L_z

[L_y,L_z]=L_x

[L_z,L_x]=L_y (19.9)

so we find that L_x , L_y and L_z are incompatible obserables. So what about [L²,L_z] ?

[L²,L_z]=[(L_x²+L_y²+L_z²),L_z]

[L²,L_z]=0

it can also be shown that

[L²,L_x]=0

[L²,L_y]=0

[L²,L_x]=[L²,L_y]=0 (19.10)

The total angular momentum is compatible with each individual component (provided that we only look at one component).

We have the simultaneous eignestates of L² and L_z , but if we try to measure (say L_x ) we destroy our information about L_z .