Previous Contents Next

Chapter 17   Lecture 16 - Review of The Quantum Mechanics of One Dimensional Systems

17.1   Symmetry of Wavefunctions

This is relevent for the The energy eignefunctions have definite symmetry

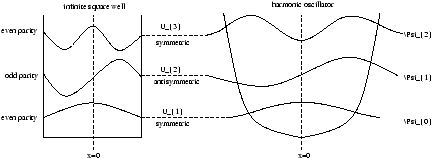
Figure 16.1 - Wavefunction Symmetry
The expectation value fo <x> is zero (by inspection)
<x >= ó
õ
¥


-¥
Yn*(x)xYn(x)dx=0  (harmonic oscillator)     (17.1)
where Yn* and Yn(x) are of even parity whilst x is of odd parity so it equals zero. This is the same for the infinite square well. We find that we obtain zero for <px> aswell.

However <x2> and <px2> remain finite.

17.2   Uncertainity Relations in Quantum Wells

We recall that
D A=<A2>-<A>2     (17.2)
for D x+D p we have established for these quantum wells
<x>=<px>=0     (17.3)

17.2.1   Example - A Quantum Harmonic Oscillator

To evaluate <px2> and <x2> we can use the ladder operators since
px=-
1
2
mw
(A-A
 
 
)     (17.4)
x=
2mw
(A+A
 
 
)     (17.5)
and so it follows from the definitions b , A and A in equation III.47
px2=-
1
2
mw æ
è		 (A)2-AA
 
 
-A
 
 
A+(A
 
 
)2 ö
ø		     (17.6)
x2=
2mw
æ
è		 (A)2+AA
 
 
+A
 
 
A+(A
 
 
)2 ö
ø		     (17.7)
Its easy to determine the action of these operators on the energy eigenstates of the Quantum Harmonic Oscillator Yn
<x 2>= ó
õ
¥


-¥
Yn*(x)x2Yn(x)dx=
mw
æ
ç
ç
è		 n+
1
2
ö
÷
÷
ø		     (17.8)
<p x2>= ó
õ
¥


-¥
Yn*(x)px2Yn(x)dx= mw æ
ç
ç
è		 n+
1
2
ö
÷
÷
ø		     (17.9)
For n=0
<kinetic energy>=
<px2>
2m
=
w
4
<potential energy>=
1
2
mw2<x2>=
w
4
total energy=<ke>+<pe>=
w
2
  (zero point)     (17.10)
D x=<x2>-<x>2=
mw
n+
1
2
D px=<px2>-<px>2= mw
n+
1
2
hence we obtain
D xD px= æ
ç
ç
è		 n+
1
2
ö
÷
÷
ø
2
    (17.11)

17.3   Dynamics of Superposition of Energy Eigenstates

For an eigenstates <E>=En for a superposition
Y (x)=
 
å
n
cnY (x)
<E >=
 
å
n
|cn|2En
for example Quantum Harmonic Oscillator states
Y (x)=
1
3
Y0(x)+
1
3
Y1(x)+
1
3
Y3(x)
<E>=
1
3
×
w
2
+
1
3
×
3
2
w +
1
3
×
11
2
w =
15
6
w
we now consider time dependence
Y (x,t)=
 
å
n
cnYn(x)e
- æ
ç
ç
è
En
 
ö
÷
÷
ø		 t
 
<E >=
 
å
n
|cn|2En=constant
where |cn|2 is time independent. <x> depends on whether the Y (x) is a superposition of only odd (or even) parity eignestates or a mixture of odd and even parity states.
x=x® odd function
for example
Y (x)=
1
2
(Y0(x)+Y1(x))
<x >= ó
õ
¥


-¥
xY*(x)Y (x)dx
<x >µ ó
õ
¥


-¥
[ xY0*Y0+Y0*xY1+Y1*xY0+Y1*xY1 ] dx
bearing in mind that (odd)× (odd)× (even)=(even) we obtain a non-zero value for <x> .
Previous Contents Next