Previous Contents Next

Chapter 14   Lecture 13 - Quantum Harmonic Oscillator

Many real potentials at least approximate to the classical harmonic oscillator

14.1   Harmonic Oscillator Potential

Many systems behave like this such as
classical:
springs, pendulums, etc
quantum:
molecules, lattice's, etc
these can be described by a force ( F ) of the form
F=-kx     (14.1)
where k is the force constant and x is the displacement.

This corresponds to a potential (we recall that F=-dV(x)/dx )
V(x)=
1
2
kx2     (14.2)
or in terms of the natural frequency
w =
k
m
V(x)=
1
2
mw2x2     (14.3)

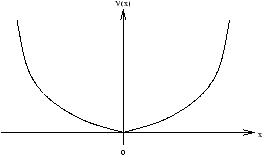
Figure 13.1 - Parabolic Potential
this potential is universal and describes:

14.2   Quantum Harmonic Oscillator

Taking the form of this potential V(x)=1/2mw2x2 we can write the (one dimension) time independent Schrödinger Equation.
æ
ç
ç
è		 -
2
2m
d2
dx2
+
1
2
mw2x2 ö
÷
÷
ø		 Yn(x)=EnYn(x)     (14.4)
The first term behaves like the momentum of the particle whilst the second term is like the position. n labels the nth energy eigenstate.

To aid in the solution we define a scaled energy:
en=
En
w
    (14.5)
we will also define a scaled displacement
b=
mw
 
x     (14.6)
the scaled displacement means that
d
dx
º
mw
 
d
db
and also that
d2
dx2
=
mw
 
d2
db2

So equation III.43 can recast in a simplified form:
1
2
æ
ç
ç
è		 b2-
d2
db2
ö
÷
÷
ø		 Yn(b )=enYn(b )     (14.7)

14.3   Ladder Operators

We adopt a method of solution that is b is the scaled position operator whilst d/db is the scaled momentum operator. We now construct two new operators A and A
A=
1
2
æ
ç
ç
è		 b+
d
db
ö
÷
÷
ø		 A
 
 
=
1
2
æ
ç
ç
è		 b-
d
db
ö
÷
÷
ø		     (14.8)
we wish to evaluate the products AA and AA . We recall the rules for manipulating operators
d
db
bº
d
db
( bf(b ) ) =b
d
db
f(b )+f(b )
hence
d
db
b=b
d
db
+1

NOTE: from onwards the hats on the b 's and d/db will be dropped

By using this result we can evulate AA and AA
AA
 
 
=
1
2
æ
ç
ç
è		 b2-
d2
db2
+1 ö
÷
÷
ø		 A
 
 
A=
1
2
æ
ç
ç
è		 b2-
d2
db2
-1 ö
÷
÷
ø		     (14.9)
note that AAAA , they don't commute.

From this we see that we can write the reduced Schrödinger Equation (equation II.46) in two ways
æ
ç
ç
è		 A
 
 
A+
1
2
ö
÷
÷
ø		 Yn(b )=enYn(b ) æ
ç
ç
è		 A
 
 
A-
1
2
ö
÷
÷
ø		 Yn(b )=enYn(b )     (14.10)
we see that these products AA and AA are closely related to the Hamiltonian H of the harmonic oscillator.
H~
1
2
mw2x2-
2
2m
d2
dx2
AA
 
 
~ (position)2+(momentum)2
Previous Contents Next