Previous Contents Next

Chapter 13   Lecture 12 - Potential Steps, Barriers and Tunneling

13.1   Potential Step

a free particle wave is incident onto a step potential, so we get a possible reflection and tranmission quantity.

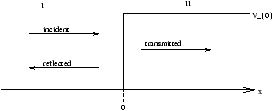
Figure 12.1 - Particle Wave Incident onto a Step Potential
In Region I:
YI(x)=Ae
kIx
 
+Be
- kIx
 
    (13.1)
where A is involved in the incident part of the wave equation whilst the B quantity is involved in the reflected part. Also
kI2=
2m
2
E     (13.2)
In Region II:
YII(x)=Ce
kIIx
 
    (13.3)
where C is involved in the transmitted part of the wave equation whilst
kII2=
2m
2
(E-V0)     (13.4)

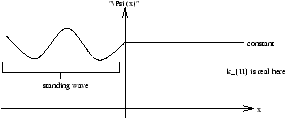
Figure 12.2 - The Wave Equation for a Step Potential when E<V0
The standing wave is due to the interference between the incident and reflected parts of the particle wave.

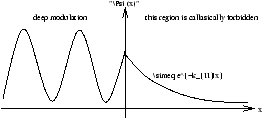
Figure 12.3 - The Wave Equation for a Step Potential when E>V0
But for E>V0 what are the reflection and transmission probabilities? Since Y (x) is continuous at x=0
A+B=C     (13.5)
since dY (x)/dx is also continuous at x=0
kIA- kIB= kIIC     (13.6)
a rearrangement of the above
A= æ
ç
ç
è		 1+
kII
kI
ö
÷
÷
ø
C
2
B= æ
ç
ç
è		 1-
kII
kI
ö
÷
÷
ø
C
2
    (13.7)
we now define the:
reflection coefficient (R)=
reflected flux
incident flux
    (13.8)
flux=(particle density)× (velocity)
for example
reflected flux=|Be
- kIx
 
|2×
kI
m
    (13.9)
so we now have the reflection coefficient to be
R=
|B|2
kI
m
|A|2
kI
m
= æ
ç
ç
è
kI-kII
kI+kII
ö
÷
÷
ø
2



 
    (13.10)
and now we have the transmission coefficient ( T ) to be
I=
|Ce
kIIx
 
|×
kII
m
|Ae
kIx
 
|×
kI
m
=
4kIkII
(kI+kII)2
    (13.11)
and to conserve probability we have
R+T=1     (13.12)

13.2   Barriers and Tunneling


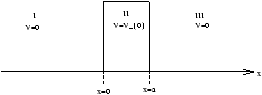
Figure 12.4 - A Particle Wave Incident on a Potential Barrier
now for E<V0 we get kII to be imaginary

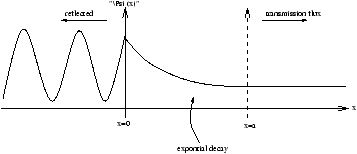
Figure 12.5 - Potential Barrier When E<V0
This process is called Quantum Mechanical Tunneling and is important in many applications such as: By applying the usual boundary conditions at regions I/II and regions II/III boundaries it can be shown
T=
1
1+
V02sinh2(g a)
4E(V0-E)
    (13.13)
where
g2=-
2m
2
(E-V0)=-kII2     (13.14)
and is known as the exponential decay constant.

for when:
g a<<1 (thin/low barrier):
sinh2(g a)® 0
T=1     (13.15)
g a>>1 (high/wide barrier):
this means there is a low barrier penetration probability
sinh2(g a) µ e
2g a
 
T~
16E(V0-E)e
-2g a
 
V02
    (13.16)

13.2.1   The Process Of Alpha-Decay

V
 
a
=VN-VC
where VN is the nuclear term and VC is the Coulomb replusion term which is proportional to (Z-2)e2/r

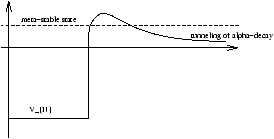
Figure 12.6 - a -Decay Process
so
T~
16E(V0-I)e
-2g a
 
V2
remember that the half life is proportional to 1/T so for some isotope A
g a~ 2.5® Thalf~ 1 second
and for some isotope B say where g a is double this
Thalf=1× e25 seconds~ 2283 years
Previous Contents Next