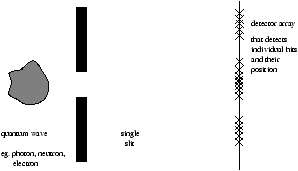Chapter 2 Lecture 2 - Uncertainity and Quantum Waves
2.1 Properties of Classical Waves
2.1.1 Principle of Superposition
From the linearity of the wave equation it follows that at any point in space and time ( r , t ) the total amplitude is the sum of the contributing amplitudes.
A(r,t)=A1(r1,t)+A2(r2,t)+... (2.1)
This leads to interference phenomena and can also apply to matter waves
2.1.2 Bandwidth Theorem and Diffraction
Consider an electromagnetic pulse A(t)
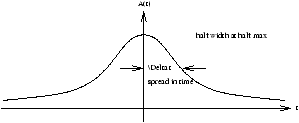
Figure 2.1 - An Electromagnetic Pulse
This can be constructed from an infinite sum of monochromatic components.
|
A(t)= |
|
ansin(wnt) |
= |
ó
õ a(w )sin(w t)dw (2.2) |
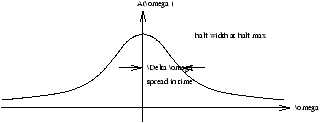
Figure 2.2 - Pulse Spectrum
Equation 1.9 is a Fourier Transform linking w and t to a Fourier Pair. A mathematical property constraining Dw anf D t is
DwD t a (2.3)
a is a number of order 1
(Gaussians 1/2 ) ® bandwidth limit or transform limit. Other quantities like x and k form an analagous pair and so likewise there will be a limit on the product
D kD x a (2.4)
This is an equation describing diffraction
To relate to matter waves we can use relations in equation 1.7 (de Broglie's Postulate)
|
E=w Þ D ED t |
|
p= k Þ D pD x |
|
(2.5) |
2.2 Diffraction of a Quantum Wave
2.2.1 A Classical Wave
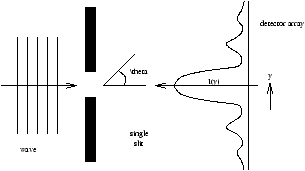
Figure 2.3 - Classical Diffraction Experiment
intensity µ |amplitude|2
Þ Iµ E2 (field amplitude)
|
I(q )µ sinc2 |
æ
ç
ç
è |
|
sinq |
ö
÷
÷
ø |
(2.6) |
2.2.2 A Quantum Wave
In QM we often deal with single particle matter waves therefore we call these quantum waves.
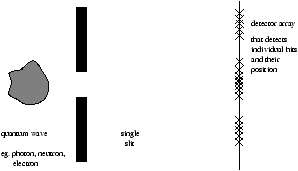
Figure 2.4 - Quantum Diffraction Experiment
After some time and by summing the number of hits in a single place across the plain of the detector array we recreate
and as for the probability for a single particle
|
P(q )µ sinc2 |
æ
ç
ç
è |
|
sinq |
ö
÷
÷
ø |
(2.7) |
probabilityµ|amplitude|2
2.3 Wave Function of a Matter Wave
Using this probabilistic interpretation we postulate the probability amplitude f(r,t) of a matter wave will be related to the probability of finding a particle at location ( r , t ).
P(r,t)=|f(r,t)|2=f(r,t)f*(r,t) (2.8)
For a beam of particles of definite momentum p that propagate freely in the x direction, what is f(x,t) ? This means that is p is definite then from the uncertainity principle
we can see all x values are equally probable as D p=0 .
A mathematically consistent form is
P(x,t)=f(x,t)f*(x,t)=A2
because