| vp= |
|
=c |
æ ç ç ç ç ç è |
1- |
æ ç ç è |
|
ö ÷ ÷ ø |
|
ö ÷ ÷ ÷ ÷ ÷ ø |
|
³ c (6.8) |
| vg= |
|
=c |
æ ç ç ç ç ç è |
1- |
æ ç ç è |
|
ö ÷ ÷ ø |
|
ö ÷ ÷ ÷ ÷ ÷ ø |
|
£ c (6.9) |
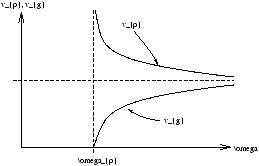
Figure 6.1 - We Note That vpvg=c2



| me |
|
=-eE- |
|
(6.1) |
| E | µ e |
|
| v | Eµ e |
|
| -w meve=-eE- |
|
| ve= |
|
| jf= |
|
(6.2) |
| jf= |
æ ç ç è |
|
ö ÷ ÷ ø |
E=sE |
| jf= |
|
E (6.3) |
| s = |
|
(6.4) |
| Ñ2E=µ0s |
|
+µ0e0 |
|
| Ñ2E=µ0 |
æ ç ç è |
|
ö ÷ ÷ ø |
|
+e0µ0 |
|
| E=E | 0e |
|
(6.5) |
| -k2E= |
|
(-w )E-e0µ0w2E |
| -k2= |
|
- |
|
| k= |
|
(w2-wp2) |
|
(6.7) |
| vp= |
|
=c |
æ ç ç ç ç ç è |
1- |
æ ç ç è |
|
ö ÷ ÷ ø |
|
ö ÷ ÷ ÷ ÷ ÷ ø |
|
³ c (6.8) |
| vg= |
|
=c |
æ ç ç ç ç ç è |
1- |
æ ç ç è |
|
ö ÷ ÷ ø |
|
ö ÷ ÷ ÷ ÷ ÷ ø |
|
£ c (6.9) |

| np= |
|
~ 9N Hz |
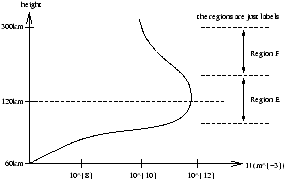
| nion= |
|
= |
æ ç ç è |
1- |
|
ö ÷ ÷ ø |
|
<1 |
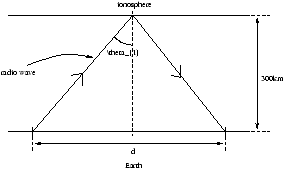
| qI>sin-1 |
|
=qC |
| R~ 1- |
|


