Previous Contents Next

Chapter 3   Electromagnetic Waves in a Vacuum

3.1   Wave Equation for Electromagnetic Waves in a Vacuum

Maxwell's Equations in a vacuum
rf=0,  jf=0,  e =e0,  µ =µ0
Ñ .E=0     (3.1)
Ñ .H=0     (3.2)
Ñ×E=-µ0
H
t
    (3.3)
Ñ×H=e0
E
t
    (3.4)
if we take the curl of Faraday's Law then we obtain
Ñ× (Ñ×E)=-Ñ2E+Ñ (Ñ .E)
Þ Ñ× (Ñ×E)=-µ0
t
Ñ×H
So
Ñ .E,  Ñ×H=e0
E
t
if we substitute in to get
Ñ2E=e0µ0
2E
t2
    (3.5)
this shows us that we can get a wave equation of electric fields. The general wave equation for Y is
Ñ2y =
1
v2
2y
2t
where v is the wave propagation speed. So an electromagnetic wave has
v=
1
µ0e0
=c     (3.6)
we can do exactly the same for the magnetic field
Ñ2H=
1
c2
2H
t2
    (3.7)
this is the wave equation for magnetic fields.

3.2   Properties of Electromagnetic Waves in a Vacuum

Consider a plane infinite sinusoidal wave
E(x,t)=E0cos(kx-w t)
where k=2p/l  m-1 and is known as the wave vector. w =2pn  s-1 is the angular frequency.
E0=E0xx+E0yy+E0zz     (3.8)

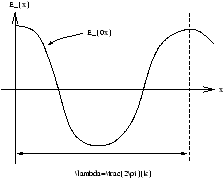
Figure 3.1 - ???
also
H=H0cos(kx-w t-f)
Þ H0=H0xx+H0yy+H0zz     (3.9)
where f is the phase relation of H to E .
E0x and H0x :
longitudinal components
E0y and H0y :
transverse components
E0z and H0z :
transverse components

3.2.1   Longitudinal Nature

we now show that E and H satisfy the wave equation. To do this we substitute the electric field into the wave equation (only x-axis propagation so there are no y or z components)
Ñ2E=
2
x2
E=-k2E0cos(kx-w t)
Ñ2E=-k2E
2E
t2
=-w2E0cos(kx-w t)
2E
t2
=-w2E
and substituting in the wave equation we obtain
k2E=
w2
c2
E
so
w2=k2c2     (3.10)
this is the condition for the wave to satisfy Maxwell's Equations. This is also the same result you get with the magnetic field.

Phase fronts propagate at the speed of light.

3.2.2   Transverse Nature

The electric and magnetic fields must obey
Ñ .H=0,  Ñ .E=0
therefore
Ñ .E(x,t)=
Ex
x
+
Ey
y
+
Ez
z
however as there is no motion in the y or z component we get
Ex
x
=0
Þ -kE0xsin(kx-w t)=0
and for a none trivial solution we get that
E0x=0     (3.11)
the same is true for the magnetic field
H0x=0     (3.12)
these solutions show us that there are no electric or magnetic fields in the direction of propagation.

This allows us to conclude that the waves are transverse.

3.2.3   Phase

H=H0cos(kx-w t-f )
E=E0cos(kx-w t)
consider that
E(x,t)=E0cos(kx-w t)y
we use Faraday's Law to obtain H
H
t
=-
1
µ0
Ñ×E=-
1
µ0
Ey
x
z
H
t
=
k
µ0
E0sin(kx-w t)z
we integrate with respect to time
H(x,t)=
kE0
µ0w
cos(kx-w t)z+constant
however the constant can be set to zero as its an unchanging magnetic field constant. So we can conclude that f =0 and so Ey and Hz are in phase and also we find that after the calculation that Ez and Hy are in phase too.

There is no connection between Ey , Ez , etc. So Ey and Ez can be of arbitrary phase in respect to one another. This is usually the case (see section 3.5).

3.2.4   Orthogonal

E and H are orthogonal

3.2.5   Direction of Energy Flow

N=E×H=Ey+Hz
y×z=x
N=Nx
The energy flow is in the direction of propagation.

3.2.6   The Ratio of The Electric and Magnetic Field

Ey
Hz
=
E0cos(kx-w t)
æ
ç
ç
è
kE0
wµ0
ö
÷
÷
ø		 cos(kx-w t)
=
µ0
e0
=Z0=377W
this is because w/k=c . The ratio of the fields are a constant. This constant is the wave impedance in a vacuum.

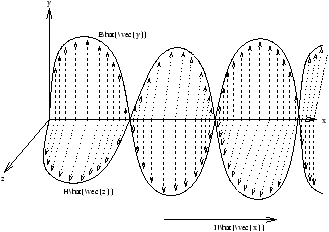
Figure 3.2 - The Structure of an Electromagnetic Wave

3.3   Radiation Pressure

3.3.1   Momentum in an Electromagnetic Wave

We have p (momentum)= k . A Photon has E (energy)=w and w/k=c and so we get
p=
E
c
kgms-1
The momentum density is equal to np where n is the number of particles per unit volume. This easily becomes nE/c . We can also so that the energy density ( U ) is nE ( U defined in handout 4).
<mementum density>=
<U>
c
also we have
<N>=c<U>
and so
<momentum density>=
<N>
c2

When radiation is incident on a surface it is either absorbed or reflected and so a pressure is exerted.

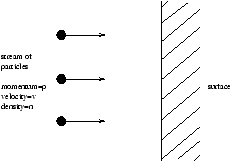
Figure 3.3 - Radiation Pressure
the flux of particles hitting the surface is nv (particles m-2s-1 ).

The momentum per particle which is given to the surface is the pressure is the force per unit area and so is flux multiplied by the change of momentum.
?? absorb reflect
pressure nvp 2nvp
EM pressure ncp 2ncp
pressure <N>/c 2<N>/c
pressure <U> 2<U>
where
<U>=
e0E02
2

comets (Problem Sheet 3):
solar sail:
to go out in the solar system system
outward force (radial pressure)=radial pressure A
where the outward force is more than the inward gravitational force and A is the area of the sail

3.4   Wave Polarisation

Example:
Ey=Ey0cos(kx-w t)
Ez=Ez0cos(kx-w t-f)
what we want to know is how the electric field behaves with time

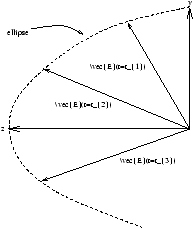
Figure 3.4 - ???
The electric field traces out a line in the y-z plane
linear polarisation:
we set f=0 and that Ey and Ez are in phase

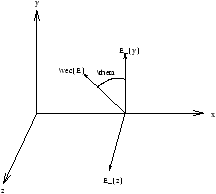
Figure 3.5 - Linear Polarisation (y-z plane)
q =tan-1
æ
ç
ç
è
Ez
Ey
ö
÷
÷
ø
q =tan-1
æ
ç
ç
è
Ez0
Ey0
ö
÷
÷
ø
we find that q is either a positive or negative constant
circular polarisation:
if f =±p/2 and Ey0=Ez0
Ey=Ey0cos( kx-w t)
Ez= Ez0sin(kx-w t)
and so the electric field vector describes a circle.
in general, electric traces an ellipse

3.5   Electromagnetic Waves in Three Dimensions


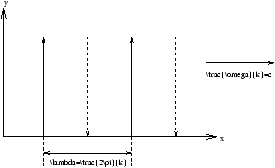
Figure 3.6 - E(x,t)=E0cos(kx-w t+f )

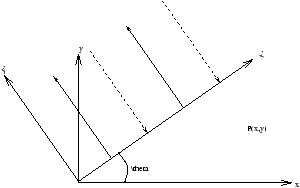
Figure 3.7 - Rotate by q
so
E=E0cos(kx'-w t)
we relate x' to x and y
x'=xcosq+ysinq
so that
E=E0cos(kxcosq+kysinq-w t)
we define the wave vector ( k ) as
k=(kx,ky,0)=(kcosq,ksinq,0)
r=(x,y,z)
Þ E=E0cos(k.r-w t)
In three dimensions it is the same technique that is used
E=E0cos(k.r-w t)
E=E0cos(kxx+kyy+kzz-w t)

3.6   Electromagnetic Waves in Complex Notation

In general
E=E0cos(k.r-w t+f )
By using De Moivre's Theorem
e
q
 
=cosq+sinq
Þ E(r,t)=Â{E 0e
(k.r-w t+f)
 
}
where  is taking the real part of the contents of the brackets.
E(r,t)=Â{E 0e
f
 
e
(k.r-w t)
 
}
We now define a new quantity called the complex field vector.
E(r,t)=E 0'e
(k.r-w t)
 
where
E0'=E 0e
f
 
The complex amplitude vector contains direction, amplitude and phase of the electric field. If we drop the prime so that
E=E 0e
(k.r-w t)
 
where E0 is a complex number which represents the complex amplitude vector.

The recovery of the physical fields is covered in Problem Sheet 4.

3.6.1   Wave Equation in Complex Notation

By using complex notation the calculus is removed and replaced with algebra.
/ t :
E/ t=-wE0e (k.r-w t)
E
t
=-wE
we have just replaced / t by -w .
Ñ . :
Ñ .E= Ex/ x+ Ey/ y+ Ez/ z
Ñ .E=
x
æ
è		 E0xe
(kxx+kyy+kzz-w t)
 
ö
ø		 +
(E0x... )+
z
(E0z... )
Ñ .E = kxE0xe
(k.r-w t)
 
+ kyE0ye
(k.r-w t)
 
+ kzE0ze
(k.r-w t)
 
Ñ .E=k.E
so we simply exchange Ñ . with k.
Ñ× :
Ñ×E=k×E so we simply exchange Ñ× with k×
Ñ2 :
Ñ2E=k.kE
Ñ2E=-k2E
so we simply exchange Ñ2 with -k2

3.6.2   Maxwell's Equation

so in light of the previous subsection we now can rewrite some equations
E=E 0e
(k.r-w t)
 
H=H 0e
(k.r-w t)
 
Gauss:
Ñ.E=0
Þ k.E=0
No Monopoles:
ie. transverse waves
Ñ .B=0
Þ k.B=0
Faraday:
Ñ×E=-µ0H/ t
Þ k×E=wµ0H
so
H=
k×E
wµ0
Ampere-Maxwell:
Ñ×H=e0E/ t
Þ k×H=-we0E
so
E=
H×k
we0
Substitute Ampere-Maxwell into Faraday:
H=
k.E
wµ0
=
k× (H×k)
w2e0µ0
H=
c2
w2
( k2H-k.H.k )
however as the waves are transverse the second term is zero and our solution becomes
w2=k2c2
this is the equation of an Electromagnetic Wave
Previous Contents Next