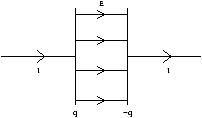
Figure 2.1 - A Capacitor ( Q=CV )




| electrostatic energy= | ó õ VdQ= |
|
CV2 (2.1) |
| C= |
|
(Problem Sheet One) |
|
CV2= |
|
× (volume) |
| UE= |
|
Jm-3 (2.2) |
| UE= |
|
(2.3) |
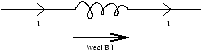
| magnetic energy=- | ó õ |
VIdt= | ó õ |
|
(LI)Idt= |
|
LI2 |
|
LI2= |
|
× (volume) |
| UM= |
|
Jm-3 (2.4) |
| UM= |
|
(2.5) |
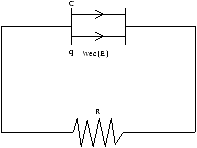
| - |
|
= | ó õ |
Rdt + |
|
N.dS (2.6) |
| W= | ó õ |
|
æ ç ç è |
|
+ |
|
ö ÷ ÷ ø |
dt (2.7) |
| ó õ |
|
Rdt = | ó õ |
|
rfE.vdt |
| ó õ |
|
Rdt = | ó õ |
|
jf.Edt (2.8) |
| N.dS=- |
|
ó õ |
æ ç ç è |
|
+ |
|
ö ÷ ÷ ø |
dt - | ó õjf.E |
| N.dS | =- | ó õ |
|
æ ç ç è |
eE. |
|
+ |
|
B. |
|
ö ÷ ÷ ø |
dt- | ó õj |
fdt =- | ó õ |
|
æ ç ç è |
E. |
é ê ê ë |
jf. |
|
ù ú ú û |
+H. |
|
ö ÷ ÷ ø |
dt |
| ... =- | ó õ |
|
(E.Ñ×H-H.Ñ×E)dt |
| N.dS | = | ó õ |
|
Ñ.(E×H)dt |
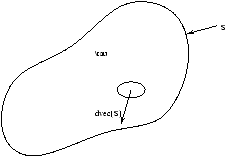
| B.dS | = |
|
(E×H).dS |
|
N.dS | = | ó õ |
|
Ñ .Ndt |
|
+ | ó õ |
|
jf.E | .dt + | ó õ |
|
Ñ .Ndt =0 (2.10) |
|
æ ç ç è |
|
+ |
|
ö ÷ ÷ ø |
+Ñ .N+jf.E=0 (2.11) |
| ó õjf.Edt |
| jf= |
|
, E= |
|
, t =Al |
| P= |
|
. |
|
.Al=IV |
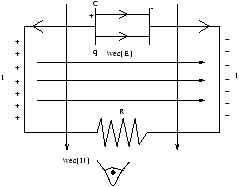
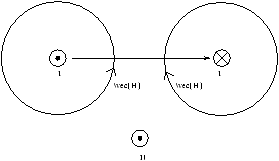
| H= |
|
q |
| N=E×H= |
|
E |
|
N.dS= |
|
E.2p rl |
| ó õN.dS=VI |
| N.dS>0 |
| N.dS<0 |


