Chapter 3 Hydrogen - Detailed Structure

The detailed spectrum of the Balmer Series ( n=2 and n=3 in hydrogen) is given on the handout figure 4.1. There is a small deviation from the theory so far, however we have made some assumptions:

non-relativistic treatment
classical electromagnetic field
nucleus is treated as a point particle

none of these assumptions are true. The proper treatment of these assumptions leads to corrections, in order of importance of the assumptions it is 1 to 3, three being the least important.

3.1 ???

3.1.1 Examples

Hydrogen in an externally applied magnetic field (ignoring spin). In the vector model, associated with l is a magnetic moment µ_l .

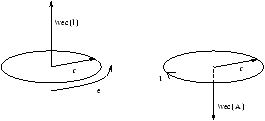
Figure 4.1 - ???

µ=IA

µ_l=-

by convention we write that

µ_l=-g_e

µ_B

l (3.1)

where

µ_B=

(Bohr Magneton) (3.2)

g_e=1

If we apply a static laboratory magnetic field to a gas of such atoms, we choose the magnetic field to be B=Bz

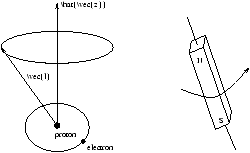
Figure 4.2 - Precession of a Atom (Bar Magnet) in a Magnetic Field

The energy of µ in B is

H'=-µB=

l.z

this technique relies on the relationships between two models

Vector Model Quantum Mechanics

l.z l_z

In Perturbation Theory the first order energy shift is

D E=<Y

nlm_l

_z|Y

nlm_l

m_l=µ_BBm_l (3.3)

The result is that the energy of a state is dependent on the orientation of the atom in space. The degeneracy with respect to m_l is lifted. This is known as the Zeeman effect. However equation 4.3 is wrong for hydrogen as we have ignored spin.

3.2 Relativistic Effects

Bohr's Model states that

e²

n 4pe₀

for n=1

e²

4pe₀ c

=a~

137

(3.4)

a is known as the fine structure constant. Since v is much less than c relativistic effects will be small. To include them there are two possibilities

do it properly from the ground up by designing a new equation that is really the Schrödinger Equation with relativistic effects included, this is known as the Dirac Equation
use the Schrödinger Equation and Perturbation Theory to include the relativistic effects as perturbations

we will be exploring the second technique.

3.2.1 Spin

Spin arises naturally in the Dirac Equation. However in non-relativistic Quantum Mechanics it must be treated as a postulate.

²c

Sm_S

=S(S+1)²c

Sm_S

(3.5)

²c

Sm_S

=m_Sc

Sm_S

(3.6)

S has only one value, for example S=1/2 but m_S±1/2 for an electron.

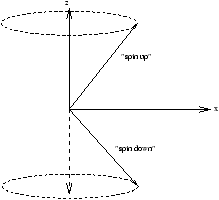
Figure 4.3 - The Vector Model For Spin

The length of the arrows in figure 4.3 is S(S+1)~ 0.866 . Since spin and orbital angular momentum are independent we write

nlm_lm_S

nlm_l

Sm_S

(3.7)

where Y_nlm_{_l} is the function in real space and c_Sm_{_S} is the spiner in spin space. By the analogy with l

µ_S=-g_S

S (3.8)

however the Dirac Equation has one more surprise. In non-relativistic Quantum Mechanics g_S=2 is a postulate. However in Quantum Electrodynamics g_S=2.00232... . For example is says that when compared with orbital angular momentum the spin gives twice as much magnetic moment for a given amount of angular momentum.

3.2.2 Addition of Angular Momentum

When there are two sources of angular momentum these can be added to find the total angular momentum, for example

j=l+s

where j is the total angularmomentum, l is the orbital angular momentum and s is the spin. We use the vector model to visulise (for example l=2 , m_l=2 , s=1/2 and m_s=1/2 )

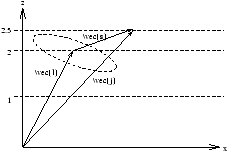
Figure 4.4 - The Vector Model For Total Angular Momentum

In figure 4.4, if we had drawn s elsewhere on its allowed cone then j would of been different. We can use operator algebra to show that: we can find the state

jm_jls

m_lm_s

m_l

m_sY

lm_lsm_s

You cannot know j , m_j , l , m_l , s and m_s all of these at the same time due to the laws of Quantum Mechanics.

²Y

jm_j

=j(j+1)²Y

jm_j

_zY

jm_s

=m_jY

jm_j

... Þ m_j=j,j-1,j-2,...

j=l+s,l+s-1,... ,|l-s|

for example j=l±1/2 or j=1/2 if l=0 .

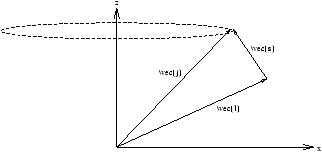
Figure 4.5 - The New Vector Model For Total Angular Momentum

In figure 4.5, the projection of s and l on the z-axis are not known. The Coupled Basis states that we don't know m_s and m_l .

3.2.3 Spin Orbit Interaction

SEE HANDOUT

E=E_n+D E

note that E_n is negative. The energy shifts up for j=3/2 however it shifts down for j=1/2 . When the energy level is high ( j=3/2 ) µ_s is roughly (symmetric) with µ_p however when the energy is low ( j=1/2 ) then µ_s is roughly ¯¯ (antisymmetric) with µ_p .

Note that:

Spectroscopic Notation:

the states are denoted by the code

(nl)^2s+1l_j

the general state has s=1/2 , l=0 and j=1/2 then the code is

(1s)²s

Selection Rules:

D j=j-j'=0,± 1

D m_j=m_j-m_j'=0,± 1

3.2.4 Other Relativistic Corrections

Two other terms appear in the Dirac Equation

relativistic mass correction
Darwin term, there is no classical picture for this

For example the n=2 level in hydrogen. The extra terms one and two make the spin-orbital more or less the same size but only the spin-orbital term splits ²p_3/2 from ²p_1/2 (see figure 4.2 ON THE HANDOUT).

Note that the spin orbit splits ²p_1/2 away from ²s_1/2 however the first and second correction terms together give a shift of ²s_1/2 that brings it back to the exact degeneracy of ²p_1/2 . The final energy including the fine structure (the result is just quoted)

E_nj=E_n

é
ê
ê
ê
ê
ê
ë

Z²a²

n²

æ
ç
ç
ç
ç
ç
è

ö
÷
÷
÷
÷
÷
ø

ù
ú
ú
ú
ú
ú
û

where a is the fine structure constant. We note that E_nj depends only on n and j and not explicitly on l .

²s

l=0, j=

²p

l=1, j=

ie. there are different values for l however the energy levels remain unchanged and we still have the same degeneracy with respect to the spectrum (see figure 4.3 ON THE HANDOUT).

3.3 Quantum Electrodynamics Effects - Lamb Shift

a tiny shift which is bigger for the s states
biggest for general states but most famous for (2s)²s_1/2
splits ²s_1/2 from ²p_1/2 , ²s_1/2 shifts up in energy by about 1.06Ghz
the electron interacts with zero-point energy of the quantised radiation field. A point like electron is smeared out where its biggest effect on the energy is where dV/dr is at a maximum.

Figure 4.6 - Quantum Electrodynamic Effects
Therefore the biggest effect for the s states is where |Y(0)|²¹ 0 , ie. the s states are smeared out so the electron sits higher in the well (see figure 4.4 ON THE HANDOUT)

3.4 Hyperfine Structure

the nucleus is not a point charge
the nucleus has angular momentum (orbital angular momentum, spin) this leads to a magnetic moment µ_I µ_I interacts with µ_j (the total magnetic moment of the electron).
see spin-orbit as a suitable analogy which leads to very small splittings in hydrogen
the general solution of hydrogen splits by 1420Mhz ie. l~ 21cm which can be used to make hydrogen lasers (the freqency standard) This is useful in astrophysics to determine the distribution of hydrogen in space (see figure 4.5 ON THE HANDOUT)

3.5 Isotopic Effects

when m is refered to it is to be replaced by the reduced mass

Different isotopes produce different reduced masses and so the overall scaling of the energy levels is around 0.05% .