Chapter 4 Two Electron Systems

Figure 5.1 - ???

r₁Þ r₁,q₁ ,f₁

r₂Þ r₂,q₂ ,f₂

r₁₂=|r₁+r₂|

He :

the nucleus is made up of either:

2p⁺+n
2p⁺+2n

Li⁺ :

the nucleus is made up of 3p⁺+3n

however Muonic Lithium is a neutral atom where 1e^- is replaced with a muon ( µ^- ). A muon has mass m_µ=207m_e and the orbit is much closer to the nucleus

r_e

207

the muon shields two electrons from the nucleus, such as the two electrons in a Z=2 core.

4.1 The Schrödinger Equation for a Two Electron System

æ
ç
ç
è

Ñ₁²

Ñ₂²

e²

4pe₀

r₁

e²

4pe₀

r₂

e²

4pe₀

r₁₂

ö
÷
÷
ø

Y =EY (4.1)

however some reduction by making things equal one turn this to

æ
ç
ç
è

Ñ₁²

Ñ₂²

r₁

r₂

r₁₂

ö
÷
÷
ø

Y =EY

this reduction can be done as we will be using atomic units

=1
4pe₀=1
m_e=1
e=1

Equation 5.1 is not exactly soluable. We need an approximation technique before we consider the relativistic effects. We note that we have used m_e=1 and are assuming that m_nucleus=¥ , also we are ignoring relativistic effects. So now we can write Equation 5.1

(H₁+H₂+H')Y =EY (4.2)

where

H₁=-

Ñ₁²

r₁

(4.3)

and similarly for the second electron. Also

H'=

r₁₂

(4.4)

4.2 Wavefunctions

If H' was small we could neglect it and attempt to write a zero-order wavefunction as

Y =Y

nlm_l

₁)Y

n'l'm'_l

(r₂) (4.5)

where Y_nlm_{_l} is the hydrogenic wavefunction with Z=2 . Then by seperating equation 5.1 into two independent hydrogen Schrödinger Equations for the electrons. The Recipe is to substitute equation 5.5 into equation 5.2 with H'=0 . We now premultiply by Y^* and integrate by dV . We use

H₁Y_n=E_nY_n

H₂Y_n'=E_n'Y_n'

Þ E⁰=E_n+E_n' (4.6)

the zero order leads us to the independent particle approximation.

4.3 Ground State of Helium

the zero-order wavefunction

Y_s=Y_1s(1)Y_1s(2) (4.7)

Y_1s=2

æ
ç
ç
è

ö
÷
÷
ø

e^-2r (4.8)

in the zero-order state ( 1/r₁₂ term is neglected) we have two electrons independently interacting with the nucleus.

E⁰=E₁+E₁=2E₁

however E_nµ Z² and Z=2 therefore

E⁰=2× (2)²E₁ (for hydrogen)

E⁰=8E₁=-108.8eV

this is the binding energy (the energy required to strip off both electrons leaving He⁺⁺ )

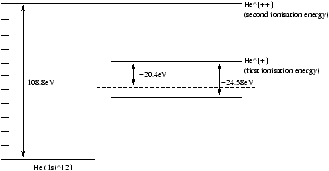
Figure 5.2 - Ionisation Energies of Helium

From figure 5.2 we find that the independent particle model is effectively useless!

Spectroscopic Notation:: Two electrons in a combined state each in a 1s hydrogenic orbital, we write this as 1s² or (1s)² .

4.3.1 Beyond the Independent Particle Approximation - General Solution

We try Perturbation Theory

E_experimental-E⁰

E⁰

79+109

-109

~ 27%

D E

(1s)²

Y_s|

r₁₂

|Y_S

(4.9)

with

Y_S=

-2(r₁+r₂)

however <1/r₁₂> is òò dr₁dr₂ . We must express 1/r₁₂ in terms of r₁ and r₂ . This gives a very messy bit of calculus. However the answer is

D E

(1s)²)

Z atomic units~ 34eV

So the total energy in respect to He⁺⁺ ionisation potential

E=E⁰+D E

(1s)²

=-108.8+34=74.8eV

The dashed line in figure 5.2 shows this result. The total energy with respect to He₊₊ ionisation potential

E_{general solution He}⁽¹⁾=-20.4eV

where the (1) is the first order perturbation theory. This is not too bad considering that H' is not small. Variational calculations would be better.

4.4 Excited States of Helium

We assume that only one electron gets excited. We will try to obtain a wavefunction that is of the form

Y₁₂=Y_1s(1)Y

nlm_l

(2) (n 1) (4.10)

The Independent Particle Approximate

E⁽⁰⁾=-

Z²

2(1)²

Z²

2n²

E⁽⁰⁾=-

Z²

æ
ç
ç
è

n²

ö
÷
÷
ø

a.u. (4.11)

For helium Z=2 for the first excited state n=2

E_(n=2)⁽⁰⁾=-

a.u.=-68eV

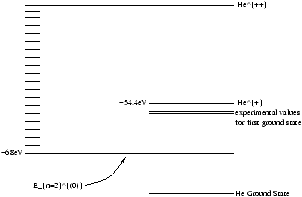
Figure 5.3 - ???

The explanation gives two states at -4.8eV and -4.0eV (with respect to the He⁺ independent particle).

4.4.1 Beyond the Independent Particle Approximation

We will try Perturbation Theory as we will expect better results than for the ground state since the percentage in the discrepancy is smaller. The inner electon shields the outer electrons from seeing the full nuclear charge, so from Perturbation Theory

D E=

Y₁₂|

r₁₂

|Y₁₂

D E=

ó
õó
õ

Y_1s^*(1)Y

nlm_l

(2)

r₁₂

Y_1s(1)Y_nlm(2)dr₁dr₂

D E=

ó
õó
õ

|Y_1s(1)|²|Y

nlm_l

(2)|²

r₁₂

dr₁r₂

This is known as the J integral. This is not related to angular momentum, however it is positiveso it shifts the energy up near to the experimental values but only in one state. How can this observed splitting occur.

4.4.2 Identical Particles

Electrons are identical, which has not been accounted for properly in our throries. So for identical particles e₁ and e₂ should be indisguishable frin Y₂₁ in every way.

If we consider hydrogen

nlm_l

|²=P₁

where P₁ is the probability that the electron is at r , q and f which can be interpreted as a charge cloud. Now we consider Helium

r₁,q₁,f₁,r₂,q₂,f₂)

|²=P₂

where P₂ is the probability that the first electron is at r₁, q₁,f₁ and the seond electon is at r₂ , q₂ and f₂ which can be interpreted as a joint probability distribution. In principle we could measure this. However are |Y₁₂|² and |Y₂₁|² the same?

When normalised and symmetrised properly, the approximate wavefunctions for the excited states of Helium may be written as

Y_S=

(Y_1s(1)Y

nlm_l

(2)+Y_1s(2)Y

nlm_l

(1))

Y_A=

(Y_1s(1)Y

nlm_l

(2)-Y_1s(2)Y

nlm_l

(1))

as an exercise you can show that

(H₁+H₂)Y_A,S=E⁽⁰⁾Y_A,S

where

E⁽⁰⁾=-

Z²

æ
ç
ç
è

n²

ö
÷
÷
ø

4.5 Perturbation Theory Using Psi-A and Psi-S

D E_S

Y_S|

r₁₂

|Y_S

D E_S=

ó
õó
õ (Y_1s^*(1)Y_nlm^*(2)+Y_1s^*(2)Y_nlm^*(1))

r₁₂

(Y_1s(1)Y_nlm(2)+Y_1s(2)Y_nlm(1))dr₁dr₂

D E_S=

ó
õó
õ |Y_1s(1)|²|Y_nlm(2)|²

r₁₂

dr₁dr

₂+

ó
õó
õY_1s^*(1)Y_nlm^*(2)Y_1s(2)Y_nlm(1)

r₁₂

dr₁dr₂

however we have seen this integrals before and we get

D E_S=J+K

also we similarly find

D E_A=J-K

where J is the J integral we obtained from Perturbation Theory whilst using Y₁₂ and Y₂₁ . K is known as the exchange integral.

The explicit calculation of J and K gives

J and K are both positive
J>K
J and K depends on n and l (however not on m_l ) so we can write them as J_nl and K_nl

we note that

J is the Coulomb interaction betwen 1s and the nl charge clouds. This describes the shielding effect
K is a measure of the likelyhood that an exchange might occur. It describes the overlap between the 1s and nl where the states are weighted by 1/r₁₂
E_S>E_A :

Y_S :
tells us that the electrons huddle and so we see an extra electron repulsion which leads to a higher energy
Y_A :
the electrons avoid one another and so the energy drops as there is less electron repulsion
the configurations have different energies, E=E_nl . In Helium we see the degeneracy with respect to l is lifted for a potential which is not simply proportional to 1/r
under high resolution Y_A splits into three states. This is a relativistic effect that depends upon spin

4.6 The Inclusion of Spin

s=1/2 for an electron. However we can have

m_s=

® spin up®a®

m_s=-

® spin down®b®¯

Figure 5.4 - l.s Forces the Use of j_m , l and s Pictures

by an analogy with j=l+s , we write

S=s₁+s₂

where S is the total spin of a two electron system.

²c

SM_S

=S(S+1)²c

SM_S

_Zc

SM_S

=m_Sc

SM_S

where c_SM_{_S} is a two electron spinor

S=s₁+s₂, s₁+s₂-1, ... ,|s₁-s₂|=1, 0

m_S=s,s-1,... ,-s

so for S=1 we get m_S=1,0,-1 . For S=0 we obtain m_S=0 .

4.6.1 Two Electon Spinors

we try simple product states

c₁=a (1)a (2)Þ

we guess that S=1 and m_S=1 for c₁ . This turns out to be a good guess

c₂=a (1)b (2)Þ ¯

c₃=b (1)a (2)Þ ¯

c₄=b (1)b (2)Þ ¯¯

we guess that S=1 and m_S=-1 for c₄ , again we find this is correct.

We note that we have guessed S and m_S . We can prove this by using operator methods (B+J, section 6.2).

c₁ and c₄ are symmetric under an exchange. c₂ and c₃ can neither be symmetric nor anti-symmetric.

The exchange of 1 and 2 in c₂ to c₃ , it can be shown (B+J) that c₂ and c₃ are not eigenfunctions of S² .

Formal Quantum Mechanics (with matrix mechanics) tell us that c₂ and c₃ are unacceptable. c must be either symmetric or anti-symetric. However c₂ and c₃ can be used to construct a pair of acceptable spinors.

c₊=

(c₂+c₃) Þ S=1, M_S=0

c_-=

(c₂-c₃) Þ S=0, M_S=0

we now group all the acceptable c 's by S so that we can get the overall spin. So for S=0 we have a singlet and so c is anti-symmetric ( S=0 and M_S=0 ). However for S=1 we get a triplet and so c₊ , c₁ and c₄ are symmetric ( S=1 and M_S=0,1,-1 respectivly).

4.7 The Pauli Exclusion Principle

We write that the total wavefunction as ( Y_total )

Y_total=Y_A,Sc

Dirac/Heisenberg:: for a system of identical particles Y_total must be either symmetric or anti-symmetric under an exchange

So a given species of particle has either Y_total to be either symmetric or anti-symmetric.

Relativistic Quantum Field Theory gives us that for particles with spin:

1/2 :: we get Fermions, for example an electron
integral:: we get Bosons

For a system of electrons Y_total must be anti-symmetric under an exchange.

This is the Pauli Exclusion Principle (in disguise, see later for the normal statement of the Pauli Exclusion Principle).

Y_total can be anti-symmetric in two ways

Y_Ac₊ , Y_Ac₁ and Y_Ac₄ where S=1 (so it forms a triplet)
Y_Sc_- where S=0 (so it forms a singlet)

4.8 Spectrum of Helium

Spectroscopic notation wil be used, upper case letters signify the angular momentum of the whole atom.

(nl,n'l')^2S+1L

for example the first excited state of Helium is

(1s 2s)¹S or (1s 2s)³S

(1s 2p)¹P or (1s 2p)³P

we note that for Helium Lº l since only one electron is excited. Also we notice that the ground state of Helium is

(1s)²'S

this means that there is no ³S state for the ground state since there is no Y_A for the ground state. The configuration splits into terms (eg. (1s 2s) , ¹S and ³S ).

By the exchange effect the energy of the term depends on the spin. This is because of the Pauli Exclusion Principle and has nothing to do with relativistic effects.

Selection Rule:: D S=0 , ie. the electric dipole operator does not act on the spin so the spin does not change

The consequences of this are

no singlet to triplet transistions are permitted, this is why we have parrallel and orthogonal helium
(1s 2s)³S is metastable