Previous Contents

Chapter 3   Stars

Most of the electromagnetic radiation energy in the Universe is emitted by stars. The elements that are fundemental to life (including oxygen and carbon) are manufactured in stars.

In developing an understanding on the structure and evolution stars we will use our Sun as a reference. The main properties of our Sun are

3.1   Stellar Interiors

3.1.1   Equation of Hydrostatic Equilibrium

How is the gravitational collapse resisted? We can consider an equation of motion of an element of fluid in the Sun's interior, however we will assume that the Sun is spherically symmetric

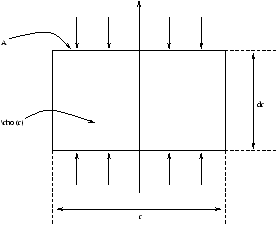
Figure 3.1 - Equation of Motion to Describe Hydrostatic Equilibrium
so from figure 3.1 we say the pressure force is acting inwards is
Ptotal=A æ
ç
ç
è		 P+
dP
dr
dr ö
÷
÷
ø
the gravitational force is
Fg=-
GM(<r)r Adr
r2
mr=-
GM(<r)r Adr
r2
+PA- æ
ç
ç
è		 PA+
dP
dr
drA ö
÷
÷
ø
by dividing through by Adr we get
rr=-
GM(<r)r
r2
-
dP
dr
so when in equilibrium, when r=0 , we get
dP
dr
=-
GM(<r)r
r2
this is the equation of hydrostatic equilibrium

3.1.2   Equation of Mass Conservation

We assume spherical symmetry and so we can write down the mass of a shell
dM=4p r2drr
dM
dr
=4p r2r
For a rough estimate of the central pressure in a solar type star (something similar to our Sun) we will assume that the density is constant
r=
M
 
 
4
3
p r
3
 
 
=1.41× 103 kgm-3
so then we can say that
M(<r)=
4
3
p r3r
with this assumption
dP
dr
=-
G
r2
4
3
p r3r2
ó
õ
 


Pc
Ps=0dP=-
4
3
p Gr2
r
2
 
 
2
=-
4
3
p G
r
2
 
 
2
M
2
 
 
æ
ç
ç
è
4
3
p r
3
 
 
ö
÷
÷
ø
2



 
Þ Pc=
3GM
2
 
 
8p r
4
 
 
=1.35× 1014 Pa~ 109 atmospheres

However to determine the termperature we need an equation of state

3.1.3   Equation of State

The Sun comprises by mass is (as a percentage)
X=0.71  Hydrogen
Y=0.27  Helium
Z=0.02  Metals
where the term metal is used to describe all the elements heavier than Helium (ie. everything except for Hydrogen and Helium).

So for these values of r and P the fluid is a plasma (ie. fully ionised) in thermal equilibrium with the radiation.

We state that the plasma behaves as an ideal gas so
P=
NkT
V
for several particles (electrons and nuclei)
P=å Pi=å
NikT
V
=å nikT
where ni is the number density of constitiment i . We need å ni and for the Sun
X=0.71=
nHmp
r
where mp is the mass of a proton (the hydrogen nuclei)
Y=0.27=
nHe4mp
r
Z=0.02=
nmetalAmp
r
where A is the typical atomic mass number of the metals. We are also ignoring the mass of the electron (as they are about two thousand times lighter than protons).

The number density of the nuclei is
nH=
r X
mp
nHe=
r Y
mp4
nmetal=
rho Z
mpA
the number density of electrons is the same as
ne=nH+2nHe+~
A
2
nmetal

 
å
ni
=
r
mp
é
ê
ê
ë		 X+
Y
4
+
Z
A
+X+
2Y
4
+
A
2
Z
A
ù
ú
ú
û
however A/Z>>0 so
 
å
ni
=
r
mp
é
ê
ê
ë		 2X+
3Y
4
+
Z
2
ù
ú
ú
û
p=
r kT
mp
é
ê
ê
ë		 2X+
3Y
4
+
Z
2
ù
ú
ú
û
now the mean particle mass is
m=µ mp=
å Nimi
å Ni
=
å nimi
å ni
=
r
å ni
where µ is the mean molecular weight, å ni=r/µ mp
å ni=
r
mp
é
ê
ê
ë		 2X+
3Y
4
+
Z
2
ù
ú
ú
û
µ=
1
2X+
3Y
4
+
Z
2
=0.61  (for our sun)
this is the equation of state
P=
r kT
µ mp
=
r kT
0.61mp
  (for our sun)
so
T=
0.61mpP
r k
however we ignore the effects of radiation pressure and so we estimate the temperature to be Tc=7.1× 106K which is a factor of two below the actual value kT~ 600eV .

Radiation

for black body radiation the energy densityso
U=aT4
where a the radiation constant and equals 4s/c so that
U=
4s T4
c
for isotropic radiation the radiation pressure is
p=
U
3
=
4s T4
3c
gas (Pa) radiation (Pa)
pressure ( Pc ) 1.35× 1014 6.4× 1011
energy density U=3/2P=2× 1014 Jm-3 U=3P=1.9× 1019Jm-3
from the table we can see that the radiation is of minor importance for the Sun's structure. For a larger mass the temperature increases and the radiation pressure begins to become important.

3.1.4   Timescales

Free-Fall Time, t-ff

In the absence of pressure a spherical cloud of particles of density r , collapses in a free fall time
tff= æ
ç
ç
è
3p
32Gr
ö
÷
÷
ø
1
2



 
  (Problem Sheet 3, Question 1)
we notice how this time is independent of the radius, for
r=1.41× 103kgm-3
Þ tff=30mins

Kelvin-Helmholtz (Gravitational) Timescale

For a star for which the radiation energy density is small it can be shown that the equation of hydrostatic equilibrium is equivalent to the Virial Theorem.
2T=-U
where in this section T is the kinetic energy. The virial theorem explains the stability, if the star contracts a little ( t~ tff ) then the potential energy falls, the kinetic energy and temperature increase, which leads to an increase in the pressure. If the star expands back then this is reversed.

Is gravity the source of the Sun's luminosity? The total energy is
E=T+U=
U
2
or U=2E and T=-E . On a longer timescale the star radiates D E (negative) then
D U=2D E,  D T=-D E
so if the star looses energy it contracts and heats up.

A star of potential energy U has radiated away U/2 , this means that for the star we can derive the luminosity L from the gravitational energy
tg=-
U
2L
~
3
5
GM2
R2L
So for the Sun tg=107 years, this is known as the Kelvin-Helmholtz timescale.

Nuclear Timescale (t-n)

In the conversion of hydrogen into helium we get 6.7MeV (or about 10-12J ) of energy per hydrogen nucleus. The Nuclear Timescale ( tn ) is the time taken for the Sun to convert 10% of its hydrogen into helium
tn=
0.1× 0.71× M
 
 
mp
×
10-12
L
=7× 109 years
As the length of the nuclear timescale is large it it sufficient to supply the energy required for the Sun's luminosity.

3.1.5   Nuclear Burning

On a timescale tg the star contracts, heating up in the process until the hydrogen in the core ignites. The reaction 4p® 4He releases 267 MeV of energy however the fusion of the nuclei is hindered by the Coulomb potential. To compute the energy production we must consider firstly the key reaction in the Sun.
p+p® d+e++ne
where d is deuteron, e+ is a positron and ne is a electron neutrino.

We wish to compute the number of nuclear reactions per second per unit volume ( R )
R=
n2
2
<s (v)v>=
n2
2mp
s (E)E
1
2
 

Fusion Cross Section (sigma(E))

We need to over come the Coulomb barrier

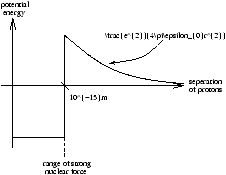
Figure 3.2 - The Coulomb Barrier
A classical calculation of the required temperature for fusion to occur
1
2
m1v2× 2~ 2×
3
2
kT=
e2
4pe0r
so for a distance of r=10-15 m the temperature is T=6× 109 K which is impossible to find occuring in the Sun.

If we make a Quantum Mechanical calculation we find that the process of Quantum Tunneling reduces the required temperature to T~ 107 K . The Quantum Mechanical solution gives the probability of barrier penetration occuring
p=Ae
- æ
ç
ç
è
EG
E
ö
÷
÷
ø
1
2



 
 
where A is a constant and EG is known as the Gamow Energy which depends on Z1 , Z2 , m1 and m2 . Z1 and Z2 are the charges on the particles and m1 and m2 are the masses of the particles.
EG=493 keV  for two protons
the probability of fusion is proportional to l2 where l is the de Broglie wavelength which is proportional to 1/E , therefore the cross section is
s (E)=
B
E
e
- æ
ç
ç
è
EG
E
ö
÷
÷
ø
1
2



 
 
where B is emperically derived from experiments.

Particle Energy Distribution

The particle energy distribution can be described by the Maxwell-Boltzmann distribution
n(E)dE=CE
1
2
 
e
-
E
kT
 
dE
<s (E)E
1
2
 
>=
ó
õ
BE
1
2
 
E
e
- æ
ç
ç
è
EG
E
ö
÷
÷
ø
 
CE
1
2
 
e
-
E
kT
 
dE
ó
õ		 CE
1
2
 
e
-
E
kT
 
dE
<s (E)E
1
2
 
>=
B ó
õ
- æ
ç
ç
è
EG
E
ö
÷
÷
ø


 
e
-
E
kT
 
dE
ó
õ		 E
1
2
 
e
-
E
kT
 
dE

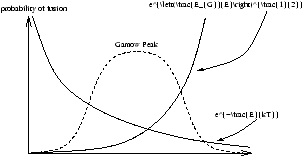
Figure 3.3 - The Particle Energy Distribution (The Fusion Probability)
This allows us to to calculate the reaction rates for any given p , T and chemical composition. The T dependence is also calculable. In the Sun there are two main processes converting hydrogen into helium.
The Proton-Proton Chain:
this reaction is important in the lower mass (cooler) stars
p+p® d+e++ne
this reaction is extremely slow and takes approximately 1010 years.
p+d® 3He+g (photon)
this reaction however is much faster taking about one second to occur. From the products of this reaction three possible further reactions (pp I, pp II and pp III) can take place to convert the 3He into 4He , however the pp I cycle is the most important reaction that takes place in the Sun
3He+3He® 4He+2p
this reaction takes about 105 years. We note that
3He =n+2p
4He =2n+2p
The CNO Cycle:
this reaction is important in the higher mass (hotter) stars where the carbon acts as a catalyst in the process
p+12C® 13N+g (photon)
where the 13N decays to
13N® 13C+e++ne
the next step in the reaction is
p+13C® 14N+g (photon)
p+14N® 15O+g (photon)
where the 15O decays to form
15O® 15N+e++ne
and finally
p+15N® 12C+4He
From a knowledge of the various reaction rates we can compute the rate of energy production per unit mass ( e (p,T,chemical composition) ). Over the interesting range of T for a proton-proton cycle
eppµ T4
and for the CNO cycle
eCNOµ T17

3.1.6   Energy Transport

Nuclear energy is generated in the core and can be transported through three methods, these will be covered in the next three subsubsections

Conduction

This is not too an important method except for in degenerate stars (such as white dwarfs), this is because the mean free path ( le ) is too small

Radiation

This is the dominant mode of transport in the Sun. In essence the photons randomly walk out, so we are interested in computing the mean free path of the photons ( l ). In reality when in thermal equilibrium where the photons interact with matter through absorption and scattering processes. The three processes important in the stellar interiors:
Thomson Scattering:
this kind of scattering involves free electrons where the direction of the photon changes however the energy does not
Bound-Free Absorption:
is the photonisation of the few neutral atoms. The reverse of this process creates new photons
Free-Free Absorption:
is the absorption of a photon by a free electron near ion. The reverse process creates photons and is known as Braßtrahlung Radiation
Since the black body spectrum is (on average) preserved, for the purposes of radiation transport, the calculations can be summarised by suitably frequency averaging the mean free path ( l ) We note that in general
l=
1
ns
and by analogy, astronomers use k (opacity) which is defines by
l=
1
rk
The results of the calculations for the solar type stars yield
k =k 'r T-3.5
for when T~ 107K and k ' is a constant for a given chemical composition, this is known as Kramer's Law

Radiative Diffusion:
we use the approximation that at any point a sixth of the photons are travelling in any of the (± x,± y,± z) directions (six possible combinations). If we consider the energy transfer across the surface at a radius r

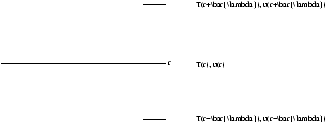
Figure 3.4 - Radiative Diffusion
So the net flux (outward+inward) is therefore
F(r)=
1
6
cu(r-l)-
1
6
cu(r+l)
u(r+l)=u(r)+
du
dr
l
F(r) =-
1
3
cl
du
dr
this can be related to the temperature gradient as
du
dr
=
du
dT
dT
dr
and for photons we know that
u=aT4
so that
du
dT
=4aT3
using all of this we obtain
L(r)=4p r2F(r)=-
1
3
4p r2cl
dT
dr
4a T3
l=
1
rk
and so finally
dT
dr
=-3r (r)k L(r)4acT3(r)4p r2
where a=4s/c

Convection

This will occur is dT/dr is sufficient negative
dT
dr
<
g -1
g
T
p
dp
dr
where g =Cp/Cv (this is covered in Problem Sheet 4) There is no complete theory of convertion for the Sun that exists. The calculation of the rate of energy transfer is uncertain in the convection zones.

3.1.7   Equation of Stellar Structure

We now have four differential equations to solve simultainously the four unknowns ( p(r) , M(<r) , L(r) and T(r) ).
  1. hydrostatic equation
    dp(r)
    dr
    		=-
    GM(<r)r(r)
    r2
  2. mass conservation
    dM(<r)
    dr
    		=4p r2r (r)
  3. energy creation, the contribution of energy to the lumonosity in a shell
    dL=4p r2r (r)e dr
    so that we obtain
    dL(r)
    dr
    		=4p r2r (r)e
  4. energy transport
    dT(r)
    dr
    		=-
    3
    4
    r (r)k L(r)
    acT3(r)4p r2
There are three subsidary relations so that
p=p(r , T, chemical composition)
which gives us an equation of state, and also we can get
k =k (r ,T,chemical composition)
e =e (r ,T,chemical composition)
as we have four equations we also require four boundary conditions so that we can satisify and solve for the unknowns
Previous Contents