Chapter 6 Lecture 6 - States and Wave Functions

6.1 States of a Quantum System

6.1.1 Quantum Eigenstates

A quantum system can be in an eigenstate of some operator - in this case a measurement of the observable yields a definite value.

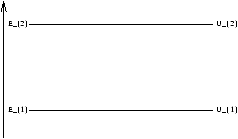
Figure 6.1 - A Two Level Atom (Two Energy Eignenstates)

If the system in figure 6.1 is prepared so that it is in state U₁ then an energy measurement will always give the value E₁ .

6.1.2 Quantum Superposition States

A quantum system can be in a state Y that is a superposition of eigenstate.

Example 1 - Superpositions of Eigenstates in a Two Level Atom

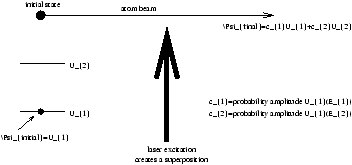
Figure 6.2 - Superpositions of Eigenstates in a Two Level Atom

The properties are

Y_initial is an eigenstate E® E₁
Y_final=c₁U₁+c₂U₂ (6.1)

A superposition of eigenstates of E , probabilities of measuring E₁+E₂ are

P(E₁)=|c₁|² P(E₂)=|c₂|² (6.2)

Imagine making many measurements of identically prepared systems we predict

<E>=å |c_n|²a_n=|c₁|²E₁+|c₂|²E₂ (6.3)

where <E> is the weighted mean, |c_n|² is the probability U_n and a_n is the eigenvalue. So the expectation value ( <E> ) of the measurement. In an experiment ( N measurements are made), then

E₁ is measured N₁ times
E₂ is measured N₂ times

N₁

~ |c₁|²,

N₂

~ |c₂|²

Example 2 - Eigenstates of a Position Measurement

A system is prepared in a state partially localized in x (to be consistent with D xD p_x/2 ). We can consider this state as a superposition of an infinite number of position eigenstates X_(x') (Dirac Delta Functions)

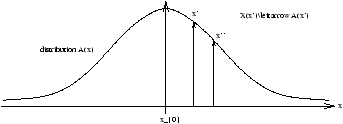
Figure 6.3 - Eigenstates of a Position Measurement (Dirac Delta Functions)

the probability of x'

P(x'® x'+dx)=|A_(x')|²dx (6.4)

where |A_(x')|² is the probability density

A(x)ºY_(x)

ie. the wavefunction is equivalent to a superposition of eigenstates of position.

6.2 Wavefunctions

Postulate B stated that the wavefunction Y (x,y,z,t) represents the probability amplitude for a position measurement at time t to find the particle at the location defined:

x® x+dx, y® y+dy, z® z+dz

So we can say

P(in volume elemental dV)=Y^*(x,y,z,t)Y(x,y,z,t)dV=|Y(x,y,z,t)|²dV (6.5)

P(in volume V)=

ó
õ

|Y(x,y,z,t)|²dV (6.6)

The probability that a particle is located somewhere in space is unity (aka 1). This leads to a normalisation requirement for a wavefunction Y(x,y,z,t) .

ó
õ

all space

Y^*(x,y,z,t)Y(x,y,z,t)dV=1 (6.7)

Imagine an un-normalised wavefunction y (r,t) we define a normalisation constant C

Y(r,t)=Cy (r,t)

|C|²

ó
õ

all space

y^*(r,t)y (r,t)dV=1

|C|²=

y^*(r,t)y (r,t)dV

(6.8)

6.2.1 A One Dimensional Example

y(x)=e

x²

a₁²

Figure 6.4 - One Dimensional Wavefunction

|C|²=

ó
õ

-¥

-2

x²

a²

dx=a

C=a

æ
ç
ç
è

ö
÷
÷
ø