

Chapter 6 Angular Momentum in Many Electon Atoms
The Hartree Self Consistent Field gives the energy of the configuration of the atom however the spectra are much more complex than this would suggest.
The configurations are often split which puts each one into a number of states the are closely spaced in energy.
Examples (of which we have already seen)
-
1s2p in helium splits to provide 3P and 1P
- 2p in hydrogen splits to provide 2p1/2 and 2p3/2
The mechanism that is present in the above examples is different for each. In the first the residual electrostatic interaction, renamed to H1
In the second example the spin orbit interaction can be generalised to a many electron system
For hydrogen and the Alkalis, the mechanism in example one does not exist so the second mechanism is dominant. However, for other many electron atoms with low to moderate Z
H1>H2
6.1 Russel Saunders Coupling Approximation
The Russel Saunders Coupling Approximation says we can assume that when H1>H2 we can neglect H2 , by using Perbubation Theorem and substituting H1 for H' we can consider H2 as a further pertubation. What representation should we use?
The first form represents new angular momenta quantities, S , L and J . This has already been seen in S=s1+s2 for a two electron system. We can use this to generalise to a many electron system
and so we now introduce
and write
where, for example
L2YL=L(L+1)2YL
LzYL=MLYz
and similar for S and J .
Quantum Mechanics limits the quantum numbers we can stipulate for a given state, for example some possible representations for a two electron system are
(nlmlms)1(nlmlms)2
(nl)1(nl2)LSMLMS
(nl)1(nl)2LSJMJ
In the absence of H1 all these representations are equally as good as each other. When H1 or H2 act we must identify constants of the motion to check which one we should use.
6.1.1 Consider Orbital Angular Momentum
Consider a two electron system where both electrons have l 0 , for example the general solution of Silicon ( [Ne]3s23p2 ) (this does not occur for helium where one electron is always in a 1s orbital)
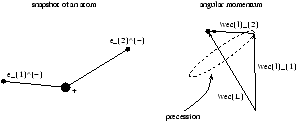
Figure 7.1 - Snaphot of an Atom and its Angular Momentum
the second electron ( e2- ) feels a torque however it also has angular momentum, when torque is present on a body with angular momentum then the object will precess about an axis. So l2 precesses, but about what axis? This argument can also be applied to e1- and l1 .
The total angular momentum must be conserved, as we are dealing with a closed system where the forces involved are internal, therefore l1 and l2 precess about L . L is a constant of the motion but l1 and l2 are not (we note that the direction may change however the magnitude does not). ?? L , Ml , l1 and l2 are good quantum numbers for ml1 and ml2 ??.
6.1.2 Consider Spin
In helium we saw that
E1=E0+Jnl± Kne
this produces a splitting effect where the singlet is S=0 and the triplet is S=1
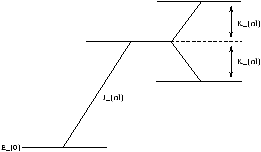
Figure 7.2 - Singlets and Triplets With Spin Consideration
We note that the terms (such as 3p and p ) depend on S through the Pauli Exclusion Principle, and singlet/triplet splitting is due to exchange. We can rewrite E1 in a form that indicates what the constants of the motion are. We use
S2=(s1+s2).(s1+s2)=s12+s22+2s1.s2
| S(S+1)= |
|
+2s1.s2 in atomic units |
E1=E0+Jnl+[1-S(S+1)]Knl
| Þ E1=E0+Jnl- |
|
[1+4S(S+1)]Knl |
S is a constant of the motion s1 and s2 are not. S , Ms , s1 and s2 are good quantum numbers however ms1 and ms2 are not.
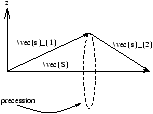
Figure 7.3 - Precession of
s1 and
s2
We can conclude that with the inclusion of hydrogen, says to use the representation
|(nl)1(nl)2LSMLMS>
and pertubation theory tends to D E to be
<LSMLMS|eij|LSMLMS>
however |LSMLMS> is a superposition of the Slater determinant Yc . We must
-
find the superposition amplitudes
- perform the integrals
from this we get the result that the configuration splits into terms
6.2 Allowed Terms in Russell-Saunders Coupling
We recall that closed shells have zero angular momentum (from the spin and orbital angular momentum)
6.2.1 Alkalis
L=l=0,1,2,...
this is a special case where the configuration is the term.
6.2.2 Helium and the Alkaline Earths
This is represented by [closed shell]ns2 which is the ground state, known as the S term. The excited states are singlets and triplets ( S=0,1 ) and again L=l=0,1,2,... (as only one electron is excited), for example
Be*º [He]2s3d
this is known as the 1D and 3D terms.
6.2.3 Other Atoms
Another example is Silicon where [Ne]3s23p4p
L=l1+l2
from vector addition and
L=l1+l2, l1+l2-1, ... ,|l1-l2|
for 3p4p we get L=2,1,0 and S=0,1 so we get six terms
3D, 3P, 3S1
1D, 1P, 1S1
all these terms have different energies. The special case is, for example, the ground state of Silicon 3p2 with which we get equivalent electrons.
For similar reasons, the ground state of helium is where the 3S state is missing which results in some terms being also missing. So only 3P , 1S and D occur.









