Chapter 5 Molecular Bonds
5.1 Molecular Bonds
SEE HANDOUT
5.2 Interatomic Potentials
The attractive potential due to single opposite charges (eg. the attraction in ionic bonds, see section 5.1) is proportional to -1/r . A general form of Uattractive is
The repulsive force between atoms comes about due to the eletrostatic repulsion between the electron clouds and also the Pauli Exclusion Principle which states that no two electrons can occupy the same quantum mechanical state in a given system. Experimentally it is found that the repulsive potential ( Urepulsive ) is
Thus a general form of the potential function is
|
U(r)=e |
é
ê
ê
ê
ê
ê
ë |
æ
ç
ç
è |
|
ö
÷
÷
ø |
|
- |
|
æ
ç
ç
è |
|
ö
÷
÷
ø |
|
ù
ú
ú
ú
ú
ú
û |
(5.1) |
| |
|
é
ê
ê
ê
ê
ê
ë |
- |
æ
ç
ç
è |
|
ö
÷
÷
ø |
|
+ |
æ
ç
ç
è |
|
ö
÷
÷
ø |
|
ù
ú
ú
ú
ú
ú
û |
=0 |
total energy=U0+K
at r=r0 the molecules have potential energy U0 and kinetic energy K .
Figure 5.1 - Symbolising Potential Energy of a Solid at Rest
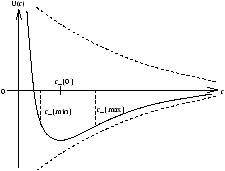
Figure 5.2 - The Electrostatic Potential Near Molecules
At r=rmin or r=rmax the potential energy is at a maxium ( U0+K ) whilst the kinetic energy is zero. If U0+K>0 then rmax®¥ and the solid melts. To calculate the latent heat of fusion we need to allow for the fact that an atom will interact with n1 nearest neighbours, n2 next nearest, etc. For a Van der Waal's Solid only the nearest neighbours are significant. So the molat latent heat of fusion is
The factor of a half is present as it refers to a pair of atoms.
5.3 Energy Bands
An atom contains electrons which occupy distinct energy levels with no more than one electron in each energy state. Consider N atoms spaced far apart so that they do not interact, then there are N electrons in the same state. As the atoms move together the electrons in adjacent atoms perturb each other and the energy levels split into bands.
The band structure is a property of the extra solid (not individual atoms)
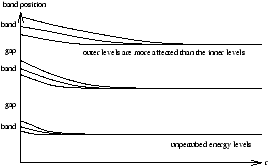
Figure 5.3 - Electron States Change Into Bands
5.3.1 Insulators
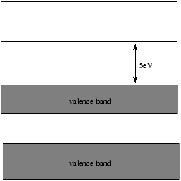
Figure 5.4 - The Bands in an Insulator
In an insulator the outer shell is full. To conduct electricity electrons in the outer most band need to go into a slightly higher energy state. In an insulator the electrons do not have sufficient energy to reach the next band so they cannot move in response to an applied electric field.
5.3.2 Semi-Conductors (Intrinsic)
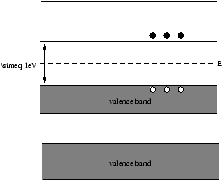
Figure 5.5 - The Bands in a Semi-Conductor (Intrinsic)
In an intrinsic semi-conductor the valence and conduction bands are close together. At high enough temperatures some electrons have sufficient thermal energy to jump into the conduction band where they are free to move in response to an electric field, eg. Ge, Si.
5.3.3 Conductors
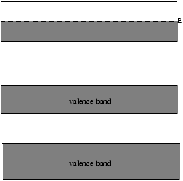
Figure 5.5 - The Bands in a Conductor
In a conductor the conduction band is only partly filled so that the electrons are free to move.
5.3.4 Resistivity
Electrons in semi-conductors and conductors can have mean free paths of more than 100r0 due to the regularity of the arrangement of the atoms (see Problem Sheet 5).
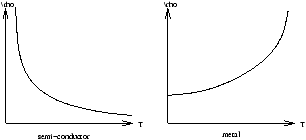
Figure 5.7 - Resistivity in Semi-Conductors and Metals
In metals as the temperature decreases the electrical conductivity increases (ie. r ( r =1/conductivity and known as the resistivity) decreases) because an electron is less likely to collide with an oscillating ion. In a semi-conductor, as the temperature decreases r increases because an electron is less likely to reach the conduction band.
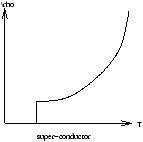
Figure 5.8 - Resistivity in a Superconductor
In some metals at a critical temperature a phase transistion takes place and r suddenly drops to zero resulting in super-conductivity.
5.4 Free Electron Model of Metals
Assume the electrons are completely inside the material, ie. they do not interact either with each other or with the lattice ions but are constrained to be within a finite volume V .
In order to find the energy distribution we need to know the density of states g(E) and the probability f(E) .
The density of states may be derived in a similar way to that for molecules in an ideal gas, so
5.4.1 Energy Distribution for Electrons
(the number of electrons with energy in the range E and E+dE in n(E)dE )
n(E)µ g(E)f(E)
where:
-
g(E) :
- is the number of states per unit energy interval
- f(E) :
- is the probability that an electron is in any particular state of energy E
| g(E)µ E |
|
(for an ideal gas) |
f(E) for electrons
For an ideal gas this was the Boltzmann factor e-E/kBT . For electrons this does not apply because the Pauli Exclusion Principle prohibits more than one electron occupying each energy state. Thus at T=0 we expect the probability distribution to be unity up to some maximum energy EF which depends on W/V .
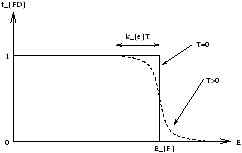
Figure 5.9 - The Fermi-Dirac Distribution
where EF is the Fermi Energy and fFD is described by Fermi-Dirac Statistics.
An electron is an example of a fermion, particles which obey the Pauli Exclusion Principle, have half-integral spin and conserve number. Other fermions include protons, neutrons, neutrinos and quarks.
Other particles are boson, they do not obey the Pauli Exclusion Principle as they have integral spin and do not conserve number. Examples of boson are photons, phonons, pions and gluons.
where A is a constant.
As shown by the formula, at high energies
| FMB(E), fFD(E), fBE(E)® e |
|
At T=0 , fFD=1 and n(E)=AE1/2 however
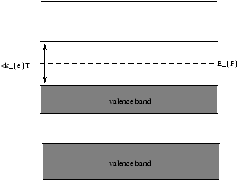
Figure 5.10 - Semi-Conductor, if this is true it will conduct electricity
5.5 Heat Capacity of Solids
Consider a mono-atomic solid, for one atom the total energy is
| |
æ
ç
ç
è |
|
mvx2+ |
|
mvy2+ |
|
mvz2 |
ö
÷
÷
ø |
+ |
æ
ç
ç
è |
|
kx2+ |
|
ky2+ |
|
kz2 |
ö
÷
÷
ø |
(vibrational kinetic energy)+(vibrational potential energy)
here we consider there is no rotation or translational energy.
From what we know from the Equipartition of Energy (see section 2.7) there are six degrees of freedom which result in
CV=3R per mole
Dulong and Petit discovered this experimentally. It holds (approximately) for all solids at high temperatures. However at low temperatures some degrees of freedom freeze out.
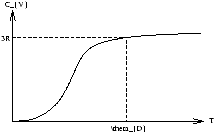
Figure 5.11 - Heat Capacity of Solids
The lowest temperature at which CV=3R is called the Debye temperature ( qD ). For example
| Solid |
Debye Temperature ( qD ) |
| Lead |
105K |
| Copper |
343K |
| Diamond |
2230K |
| |
Einstein first explained the low temperature behaviour by considering each atom to behave as an independent oscillator (fundemental frequency, see Classwork 4 or the Mechanics and Relativity Course). This is only approximately correct ecause the atoms do not act independently. Debye treated the solid as a homogeneous elastic medium. When an atom oscillates a vibrational phonon wave propagates through the solid at the speed of sound. Rigid solid with high VS leads to a high qD .
If the free electrons in a metal behaved as an ideal gas they would contribute an extra 3/2R to CV . This does not happen because the electrons obey Fermi-Dirac statistics (see section 5.4) so only a small fraction1 can contribute.
5.6 Thermal Conductivity
Consider a rod of cross-section A with one end at position x , kept at a higher temperature than the other end at x=0 .
Observations show that heat is transfered at a rate
where k is the thermal conductivity of a material.
In non-metals the heat is transferred by phonon waves propagating from the region of high T (strong vibrational) to low T (weak vibration).
In metals the phonon waves are scattered by the electrons and heat transfer is carried out by the electrons. k depends on the speed an dmean free path of the electrons specific heat.
5.7 Thermal Expansion
(eg. Lennard Jones Potential 6-12)
| U(r)=e |
é
ê
ê
ê
ê
ê
ë |
æ
ç
ç
è |
|
ö
÷
÷
ø |
|
-2 |
æ
ç
ç
è |
|
ö
÷
÷
ø |
|
ù
ú
ú
ú
ú
ú
û |
-e +K=e (y2-2y)
| Fmin=r0(1+f) |
|
=r0 |
æ
ç
ç
è |
1- |
|
f+ |
|
f2+... |
ö
÷
÷
ø |
| Fmax=r0(1-f) |
|
=r0 |
æ
ç
ç
è |
1+ |
|
f+ |
|
f2+... |
ö
÷
÷
ø |
| r= |
|
(rmin+rmax)=r0 |
æ
ç
ç
è |
1+ |
|
f2+... |
ö
÷
÷
ø |
- 1
- those within kBT of EF (see Problem Sheet 1, Question 1)